题目内容
 已知∠B=60°,∠C=40°,∠ADC=3∠A,求∠A.
已知∠B=60°,∠C=40°,∠ADC=3∠A,求∠A.考点:三角形的外角性质
专题:
分析:设∠A=a°,则∠ADC=3∠A=3a°,延长AD交BC于E,根据三角形外角性质得出∠DEC=∠B+∠A,∠ADC=∠C+∠DEC=∠A+∠B+∠C,代入得出方程3a=60+40+a,求出a即可.
解答: 解:设∠A=a°,则∠ADC=3∠A=3a°,
解:设∠A=a°,则∠ADC=3∠A=3a°,
延长AD交BC于E,
则∠DEC=∠B+∠A,∠ADC=∠C+∠DEC=∠A+∠B+∠C,
∵∠B=60°,∠C=40°,∠ADC=3∠A,
∴3a=60+40+a,
解得:a=50,
∴∠A=50°.
 解:设∠A=a°,则∠ADC=3∠A=3a°,
解:设∠A=a°,则∠ADC=3∠A=3a°,延长AD交BC于E,
则∠DEC=∠B+∠A,∠ADC=∠C+∠DEC=∠A+∠B+∠C,
∵∠B=60°,∠C=40°,∠ADC=3∠A,
∴3a=60+40+a,
解得:a=50,
∴∠A=50°.
点评:本题考查了三角形外角性质的应用,解此题的关键是得出关于a的方程,注意:三角形的一个外角等于和它不相邻的两个内角的和.

练习册系列答案
相关题目
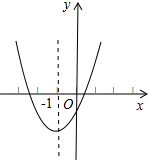 已知二次函数y=ax2+bx+c的图象如图,其对称轴x=-1,给出下列结果:
已知二次函数y=ax2+bx+c的图象如图,其对称轴x=-1,给出下列结果: 如图,过正方形ABCD的顶点作对角线BD的平行线,在这条线上取一点E,使BE=BD,连结DE,BE交AD于F,求证:DE2=EF•DB.
如图,过正方形ABCD的顶点作对角线BD的平行线,在这条线上取一点E,使BE=BD,连结DE,BE交AD于F,求证:DE2=EF•DB. 一圆柱高9cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程(π取3)是
一圆柱高9cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程(π取3)是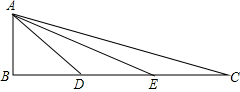 如图,在△ABC中,∠B=90°,点D、E在BC上,且AB=BD=EC=DE,求证:
如图,在△ABC中,∠B=90°,点D、E在BC上,且AB=BD=EC=DE,求证: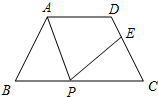 如图,在等腰梯形ABCD中,AD∥BC,AD=3,BC=7,∠B=60°,P为BC边上一点(不与B、C重合).过点P作∠APE=∠B,PE交CD于E.
如图,在等腰梯形ABCD中,AD∥BC,AD=3,BC=7,∠B=60°,P为BC边上一点(不与B、C重合).过点P作∠APE=∠B,PE交CD于E.