题目内容
在⊙O中,弦AB=6cm,圆周角∠ACB=135°,则⊙O的直径为 cm.
考点:圆周角定理,等腰直角三角形
专题:
分析:过点O作⊙O的直径AD,连接BD,根据圆周角定理可知∠ABD=90°,由圆内接四边形的性质可得出∠D的度数,进而判断出△ABD的形状,根据勾股定理即可得出即可得出结论.
解答: 解:过点O作⊙O的直径AD,连接BD,
解:过点O作⊙O的直径AD,连接BD,
∵AD是⊙O的直径,
∴∠ABD=90°.
∵∠ACB=135°,
∴∠D=45°,
∴△ABD是等腰直角三角形,
∴AB=BD=6cm,
∴AD=
=6
cm.
故答案为:6
.
 解:过点O作⊙O的直径AD,连接BD,
解:过点O作⊙O的直径AD,连接BD,∵AD是⊙O的直径,
∴∠ABD=90°.
∵∠ACB=135°,
∴∠D=45°,
∴△ABD是等腰直角三角形,
∴AB=BD=6cm,
∴AD=
| 62+62 |
| 2 |
故答案为:6
| 2 |
点评:本题考查的是圆周角定理,熟知直径所对的圆周角是直角是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
如果一个正多边形绕它的中心旋转90°就和原来的图形重合,那么这个正多边形是( )
| A、正三角形 | B、正方形 |
| C、正五边形 | D、正六边形 |
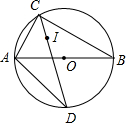 如图,AB是⊙O的直径,点C是⊙O上一点,点I是△ABC(AC<AB)的内心,CI的延长线交⊙O于点D,连AD.
如图,AB是⊙O的直径,点C是⊙O上一点,点I是△ABC(AC<AB)的内心,CI的延长线交⊙O于点D,连AD.
 已知∠B=60°,∠C=40°,∠ADC=3∠A,求∠A.
已知∠B=60°,∠C=40°,∠ADC=3∠A,求∠A.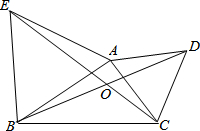 图中△ABE和△ACD都是等边三角形,BD与CE相交于点O.
图中△ABE和△ACD都是等边三角形,BD与CE相交于点O. 如图,△ABC与△DEF关于直线l成轴对称,
如图,△ABC与△DEF关于直线l成轴对称,