题目内容
10.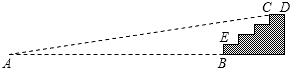 某商场门前的台阶截面如图所示,已知每级台阶的宽度(图中CD)均为0.3m,高度(图中的BE)均为0.2m.现将此台阶改造成供轮椅行走的斜坡,并且设计斜坡的倾斜角∠A为9°,计算从斜坡的起点A到台阶前点B的距离.(精确到0.1m)(参考数据:sin9°≈0.16;cos9°≈0.99;tan9°≈0.16)
某商场门前的台阶截面如图所示,已知每级台阶的宽度(图中CD)均为0.3m,高度(图中的BE)均为0.2m.现将此台阶改造成供轮椅行走的斜坡,并且设计斜坡的倾斜角∠A为9°,计算从斜坡的起点A到台阶前点B的距离.(精确到0.1m)(参考数据:sin9°≈0.16;cos9°≈0.99;tan9°≈0.16)
分析 过C作CF⊥AB,交AB的延长线于点F,根据正切的概念求出AF的长,结合图形计算即可.
解答 解:过C作CF⊥AB,交AB的延长线于点F.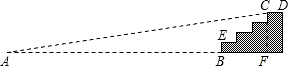 由题意得,CF=0.80m,BF=0.90m,
由题意得,CF=0.80m,BF=0.90m,
在Rt△CAF中,tanA=$\frac{CF}{AF}$,
∴AF=$\frac{CF}{tanA}$=$\frac{0.8}{0.16}$=5,
∴AB=AF-BF=5-0.9=4.1m,
答:从斜坡的起点A到台阶前点B的距离为4.1m.
点评 本题考查的是解直角三角形的应用-坡度坡角问题,掌握坡度的概念、熟记锐角三角函数的定义是解题的关键.

练习册系列答案
相关题目
18.(x-2)(x+3)的运算的结果是( )
| A. | x2-6 | B. | x2+6 | C. | x2-5x-6 | D. | x2+x-6 |
5.把$\sqrt{\frac{27}{4}}$化为最简二次根式,结果是( )
| A. | $\frac{\sqrt{27}}{2}$ | B. | $\frac{3\sqrt{3}}{\sqrt{4}}$ | C. | $\frac{3}{2}$ | D. | $\frac{3\sqrt{3}}{2}$ |
19.下列命题:
①一组对边平行,另一组对边相等的四边形是平行四边形;
②对角线互相平分的四边形是平行四边形;
③在四边形ABCD中,AB=AD,BC=DC,那么这个四边形ABCD是平行四边形;
④一组对边平行,一组对角相等的四边形是平行四边形.
其中正确命题的个数是( )
①一组对边平行,另一组对边相等的四边形是平行四边形;
②对角线互相平分的四边形是平行四边形;
③在四边形ABCD中,AB=AD,BC=DC,那么这个四边形ABCD是平行四边形;
④一组对边平行,一组对角相等的四边形是平行四边形.
其中正确命题的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
20.若-2an-1-4an+1的公因式是M,则M等于( )
| A. | 2an-1 | B. | -2an | C. | -2an-1 | D. | -2an+1 |
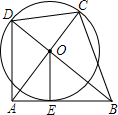 如图,Rt△AOB中,OA⊥OB,⊙O与AB相切于点E,AO、BO的延长线交⊙O于C、D.若⊙O的半径为1,求四边形ABCD的面积最小值.
如图,Rt△AOB中,OA⊥OB,⊙O与AB相切于点E,AO、BO的延长线交⊙O于C、D.若⊙O的半径为1,求四边形ABCD的面积最小值.
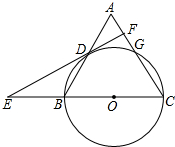 如图,在△ABC中,CA=CB,以BC为直径的圆⊙O交AC于点G,交AB于点D,过点D作⊙O的切线,交CB的延长线于点E,交AC于点F.
如图,在△ABC中,CA=CB,以BC为直径的圆⊙O交AC于点G,交AB于点D,过点D作⊙O的切线,交CB的延长线于点E,交AC于点F.