题目内容
9.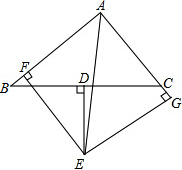 如图,△ABC中,D为BC的中点,DE⊥BC交∠BAC的平分线AE于点E,EF⊥AB于F,EG⊥AG交AC的延长线于G.
如图,△ABC中,D为BC的中点,DE⊥BC交∠BAC的平分线AE于点E,EF⊥AB于F,EG⊥AG交AC的延长线于G.(1)求证:BF=CG.
(2)求证:2AF=AB+AC.
分析 (1)连接BE、EC,只要证明△EFB≌△EGC即可.
(2)由△AEF≌△AEG,得AF=AG,由△EFB≌△EGC得BF=CG,根据线段和差定义即可解决.
解答 (1)证明: 连接BE、EC.
连接BE、EC.
∵BD=DC,DE⊥BC,
∴EB=EC,
∵EA平分∠BAC,EF⊥AB,EC⊥AC,
∴EF=EG,
在RT△EFB和RT△EGC中,
$\left\{\begin{array}{l}{EF=EG}\\{BE=EC}\end{array}\right.$,
∴△EFB≌△EGC,
∴BF=CG.
(2)证明:在RT△AEF和RT△AEG中,
$\left\{\begin{array}{l}{AE=AE}\\{EF=EG}\end{array}\right.$,
∴△AEF≌△AEG,
∴AF=AG,
∵△EFB≌△EGC,
∴BF=CG,
∴AB+AC=AF+BF+AG-CG=2AF.
即2AF=AB+AC.
点评 本题考查角平分线的性质定理、全等三角形的判定和性质、线段垂直平分线的性质等知识,解题的关键是添加辅助线构造全等三角形,需要熟练掌握全等三角形的判定,属于中考常考题型.

练习册系列答案
相关题目
4. 如图,A,B,C表示修建在一座山上的三个缆车站的位置,AB,BC表示连接缆车站的钢缆.已知A,B,C所处位置的海拔AA1,BB1,CC1分别为130米,400米,1000米.由点 A测得点B的仰角为30°,由点B测得点C的仰角为45°,那么AB和BC的总长度是( )
如图,A,B,C表示修建在一座山上的三个缆车站的位置,AB,BC表示连接缆车站的钢缆.已知A,B,C所处位置的海拔AA1,BB1,CC1分别为130米,400米,1000米.由点 A测得点B的仰角为30°,由点B测得点C的仰角为45°,那么AB和BC的总长度是( )
 如图,A,B,C表示修建在一座山上的三个缆车站的位置,AB,BC表示连接缆车站的钢缆.已知A,B,C所处位置的海拔AA1,BB1,CC1分别为130米,400米,1000米.由点 A测得点B的仰角为30°,由点B测得点C的仰角为45°,那么AB和BC的总长度是( )
如图,A,B,C表示修建在一座山上的三个缆车站的位置,AB,BC表示连接缆车站的钢缆.已知A,B,C所处位置的海拔AA1,BB1,CC1分别为130米,400米,1000米.由点 A测得点B的仰角为30°,由点B测得点C的仰角为45°,那么AB和BC的总长度是( )| A. | 1200$+270\sqrt{2}$ | B. | 800$+270\sqrt{2}$ | C. | 540$+600\sqrt{2}$ | D. | 800$+600\sqrt{2}$ |
 如图,在△ABC中,DE⊥AB,DF⊥AC,垂足分别为点E,F,AE=AF,找出一对全等的三角形,并给出证明.
如图,在△ABC中,DE⊥AB,DF⊥AC,垂足分别为点E,F,AE=AF,找出一对全等的三角形,并给出证明.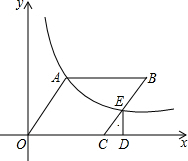 如图,在平面直角坐标系中,?OABC的顶点C的坐标为(3,0),∠AOC=45°,反比例函数y=$\frac{k}{x}$(k>0)的图象经过点A交BC于点E,过点E作ED⊥x轴于点D,ED=1.
如图,在平面直角坐标系中,?OABC的顶点C的坐标为(3,0),∠AOC=45°,反比例函数y=$\frac{k}{x}$(k>0)的图象经过点A交BC于点E,过点E作ED⊥x轴于点D,ED=1.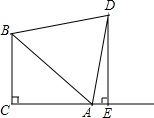 如图,△ABC中,∠ACB=90°,AC=BC,D为△ABC外一点,且AD=BD,DE⊥AC交CA的延长线于E,求证:DE=AE+BC.
如图,△ABC中,∠ACB=90°,AC=BC,D为△ABC外一点,且AD=BD,DE⊥AC交CA的延长线于E,求证:DE=AE+BC.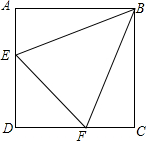 如图,点E,F分别在正方形ABCD的边AD,CD上,∠EBF=45°,连接EF,求证:EF=AE+CF.
如图,点E,F分别在正方形ABCD的边AD,CD上,∠EBF=45°,连接EF,求证:EF=AE+CF. 如图,AB=AC,D、E分别是AB、AC的中点,AM⊥CD于M,AN⊥BE干N.
如图,AB=AC,D、E分别是AB、AC的中点,AM⊥CD于M,AN⊥BE干N. 如图,在?ABCD中,BD⊥AD,AD=8,AB=10,则AC的长为2$\sqrt{73}$.
如图,在?ABCD中,BD⊥AD,AD=8,AB=10,则AC的长为2$\sqrt{73}$.