题目内容
18．若点A（x1，y1），点B（x2，y2）在双曲线y=$\frac{-1}{x}$上，若x1＞x2＞0，则y1＞ y2（填“＞”或“＜”）分析 画出图象即可确定y1、y2的大小．
解答 解：由图象可知：y1＞y2．
点评 本题考查反比例函数图象上点的坐标，解题的关键是正确画出图形，利用函数图象比较函数值大小，记住反比例函数k＞O，图象在一，三象限，k＜0图象在二四象限，属于中考常考题型．
练习册系列答案
状元坊全程突破导练测系列答案
相关题目
9．
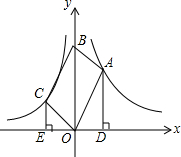在平面直角坐标系xOy中，函数y=$\frac{{k}_{1}}{x}$（k1＞0，x＞0）、函数y=$\frac{{k}_{2}}{x}$（k2＜0，x＜0）的图象分别经过?OABC的顶点A、C，点B在y轴正半轴上，AD⊥x轴于点D，CE⊥x轴于点E，若|k1|：|k2|=9：4，则AD：CE的值为（ ）
在平面直角坐标系xOy中，函数y=$\frac{{k}_{1}}{x}$（k1＞0，x＞0）、函数y=$\frac{{k}_{2}}{x}$（k2＜0，x＜0）的图象分别经过?OABC的顶点A、C，点B在y轴正半轴上，AD⊥x轴于点D，CE⊥x轴于点E，若|k1|：|k2|=9：4，则AD：CE的值为（ ）| A． | 4：9 | B． | 2：3 | C． | 3：2 | D． | 9：4 |
3．函数y=x+3与y=$-\frac{2}{x}$的图象的交点为（a，b），则$\frac{1}{a}-\frac{1}{b}$的值是（ ）
| A． | $-\frac{3}{2}$ | B． | $\frac{3}{2}$ | C． | $-\frac{2}{3}$ | D． | $\frac{2}{3}$ |
如图，已知抛物线y=ax2+$\frac{5}{2}$x+c经过A（4，0），B（1，0）两点，
已知：如图，B，A，E在同一直线上，AC∥BD且AC=BE，∠ABC=∠D．求证：AB=BD．
8．
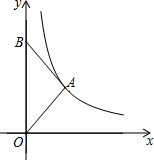如图，在平面直角坐标系中，点B在y轴上，第一象限内点A满足AB=AO，反比例函数y=$\frac{k}{x}$的图象经过点A，若△ABO的面积为2，则k的值为（ ）
如图，在平面直角坐标系中，点B在y轴上，第一象限内点A满足AB=AO，反比例函数y=$\frac{k}{x}$的图象经过点A，若△ABO的面积为2，则k的值为（ ）| A． | 1 | B． | 2 | C． | 4 | D． | $\frac{1}{2}$ |