题目内容
20．若方程x2-3x-4=0的两根分别为x1和x2，则$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$的值是（ ）| A． | 1 | B． | 2 | C． | -$\frac{3}{4}$ | D． | -$\frac{4}{3}$ |
分析 找出一元二次方程的系数a，b及c的值，利用根与系数的关系求出两根之和与两根之积，然后利用完全平方公式变形后，将求出的两根之和与两根之积代入，即可求出所求式子的值．
解答 解：依题意得：x1+x2=3，x1•x2=-4，
所以$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}•{x}_{2}}$=$\frac{3}{-4}$=-$\frac{3}{4}$．
故选：C．
点评 此题考查了一元二次方程根与系数的关系，对所求的代数式进行正确的变形是解决本题的关键．
练习册系列答案
期末集结号系列答案
相关题目
如图，已知抛物线y=ax2+$\frac{5}{2}$x+c经过A（4，0），B（1，0）两点，
8．
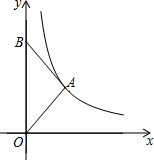如图，在平面直角坐标系中，点B在y轴上，第一象限内点A满足AB=AO，反比例函数y=$\frac{k}{x}$的图象经过点A，若△ABO的面积为2，则k的值为（ ）
如图，在平面直角坐标系中，点B在y轴上，第一象限内点A满足AB=AO，反比例函数y=$\frac{k}{x}$的图象经过点A，若△ABO的面积为2，则k的值为（ ）| A． | 1 | B． | 2 | C． | 4 | D． | $\frac{1}{2}$ |
15．
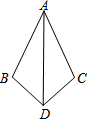如图，已知∠BDA=∠CDA，则不一定能使△ABD≌△ACD的条件是（ ）
如图，已知∠BDA=∠CDA，则不一定能使△ABD≌△ACD的条件是（ ）| A． | BD=DC | B． | AB=AC | C． | ∠B=∠C | D． | ∠BAD=∠CAD |
5．某市决定对欲引进种植的A、B两种绿色蔬果实行政府补贴．据分析得到以下两条信息：
信息一：对于A种蔬果，所获收益yA（万元）与补贴金额x（万元）之间满足正比例函数关系：yA=kx；
信息二：对于B种蔬果，所获收益yB（万元）与补贴金额x（万元）之间满足二次函数关系：yB=ax2+bx；
其中，yA、yB（万元）与补贴金额x（万元）的部分对应值如上表所示：
填空：yA=0.6xyB=-0.2x2+2.6x．
信息一：对于A种蔬果，所获收益yA（万元）与补贴金额x（万元）之间满足正比例函数关系：yA=kx；
信息二：对于B种蔬果，所获收益yB（万元）与补贴金额x（万元）之间满足二次函数关系：yB=ax2+bx；
| x/万元 | 1 | 2 |
| yA/万元 | 0.6 | 1.2 |
| yB/万元 | 2.4 | 4.4 |
填空：yA=0.6xyB=-0.2x2+2.6x．
10．袋子中装有4个黑球和2个白球，这些球的形状、大小、质地等完全相同，在看不到球的条件下，随机地从袋子中摸出三个球．下列事件是必然事件的是（ ）
| A． | 摸出的三个球中至少有两个球是黑球 | |
| B． | 摸出的三个球中至少有两个球是白球 | |
| C． | 摸出的三个球中至少有一个球是黑球 | |
| D． | 摸出的三个球中至少有一个球是白球 |