题目内容
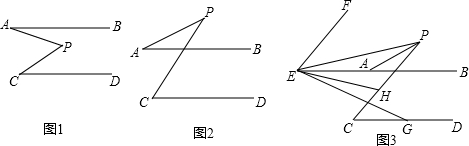
已知AB∥CD,点P为直线AB、CD所确定的平面内一点.
(1)如图1,直接写出∠P、∠A、∠C之间的数量关系;(不用写具体证明过程)
(2)如图2,求证:∠P=∠C-∠A;
(3)如图3,点E在直线AB上,若∠APC=20°,∠PAB=30°,过点E作EF∥PC,作∠PEG=∠PEF,∠BEG的平分线交PC于点H,求∠PEH的度数.
(1)如图1,直接写出∠P、∠A、∠C之间的数量关系;(不用写具体证明过程)
(2)如图2,求证:∠P=∠C-∠A;
(3)如图3,点E在直线AB上,若∠APC=20°,∠PAB=30°,过点E作EF∥PC,作∠PEG=∠PEF,∠BEG的平分线交PC于点H,求∠PEH的度数.

考点:平行线的性质
专题:
分析:(1)首先过点P作PE∥AB,则易得AB∥PE∥DE,然后由两直线平行,内错角相等,即可证得:∠A+∠C=∠P;
(2)由AB∥CD,易得∠1=∠C,然后又三角形外角的性质,证得:∠P=∠C-∠A;
(3)由三角形外角的性质,可求得∠1=50°,然后由平行线的性质,求得∠FEB=50°,再利用角平分线的性质,求得∠PEH=∠PEG-∠GEH=
(∠FEG-∠BEG)=
∠FEB=25°.
(2)由AB∥CD,易得∠1=∠C,然后又三角形外角的性质,证得:∠P=∠C-∠A;
(3)由三角形外角的性质,可求得∠1=50°,然后由平行线的性质,求得∠FEB=50°,再利用角平分线的性质,求得∠PEH=∠PEG-∠GEH=
| 1 |
| 2 |
| 1 |
| 2 |
解答: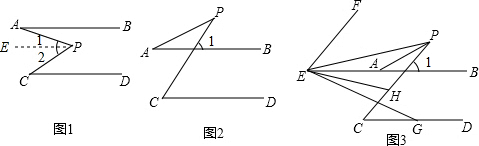 解:(1)∠P=∠A+∠C.
解:(1)∠P=∠A+∠C.
理由:过点P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD,
∴∠1=∠A,∠2=∠C,
∴∠APB=∠1+∠2=∠A+∠C;
(2)∵AB∥CD,
∴∠1=∠C,
∵∠P=∠1-∠A,
∴∠P=∠C-∠A;
(3)∵∠APC=20°,∠PAB=30°,
∴∠1=∠APC+∠PAB=50°,
∵EF∥PC,
∴∠FEB=∠1=50°,
∵∠PEG=∠PEF,∠BEG的平分线交PC于点H,
∴∠GEH=
∠BEG,∠PEG=
∠FEG,
∴∠PEH=∠PEG-∠GEH=
(∠FEG-∠BEG)=
∠FEB=25°.
 解:(1)∠P=∠A+∠C.
解:(1)∠P=∠A+∠C.理由:过点P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD,
∴∠1=∠A,∠2=∠C,
∴∠APB=∠1+∠2=∠A+∠C;
(2)∵AB∥CD,
∴∠1=∠C,
∵∠P=∠1-∠A,
∴∠P=∠C-∠A;
(3)∵∠APC=20°,∠PAB=30°,
∴∠1=∠APC+∠PAB=50°,
∵EF∥PC,
∴∠FEB=∠1=50°,
∵∠PEG=∠PEF,∠BEG的平分线交PC于点H,
∴∠GEH=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠PEH=∠PEG-∠GEH=
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题考查了平行线的性质以及三角形外角的性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
已知三角形的三边长的比是1:
:
,那么这个三角形一定不是( )
| ||
| 2 |
| 1 | ||
|
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、不等边三角形 |
 一架云梯长25米,如图所示,斜靠在一面墙上,这时梯子的顶端距地面24米.
一架云梯长25米,如图所示,斜靠在一面墙上,这时梯子的顶端距地面24米. 如图,直线a、b被直线c所截,a∥b,∠1=121°,求∠3的度数.
如图,直线a、b被直线c所截,a∥b,∠1=121°,求∠3的度数.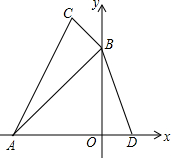 如图,在平面直角坐标系中,△ABC中点A(-3,0),B(0,3),C(-1,4),在x轴正半轴中有一个点D(1,0),连结BD,问:
如图,在平面直角坐标系中,△ABC中点A(-3,0),B(0,3),C(-1,4),在x轴正半轴中有一个点D(1,0),连结BD,问: 在一张城市地图上,有学校、医院、图书馆三地,但被墨迹污染,图书馆的具体位置看不清,但知道图书馆在学校的东北方向,在医院的南偏西75°方向,你能确定图书馆的位置吗?
在一张城市地图上,有学校、医院、图书馆三地,但被墨迹污染,图书馆的具体位置看不清,但知道图书馆在学校的东北方向,在医院的南偏西75°方向,你能确定图书馆的位置吗?