题目内容
2.为了有效保护环境,某居委会倡议居民将生活垃圾进行可回收的、不可回收的和有害的分类投放.一天,小林把垃圾分装在三个袋中,则他任意投放垃圾,把三个袋子都放错位的概率是$\frac{1}{3}$.分析 可回收的、不可回收的和有害的垃圾分别用A、B、C表示,可回收的、不可回收的和有害的分类的投放点分别用a、b、c表示,通过列表展示所有6种等可能的结果数,再找出三个袋子都放错位的结果数,然后根据概率公式求解.
解答 解:可回收的、不可回收的和有害的垃圾分别用A、B、C表示,可回收的、不可回收的和有害的分类的投放点分别用a、b、c表示,
列表如下为:
共有6种等可能的结果数,其中三个袋子都放错位的结果数为2,
所以三个袋子都放错位的概率=$\frac{2}{6}$=$\frac{1}{3}$.
故答案为$\frac{1}{3}$.
点评 本题考查了列表法与树状图法:利用列表法和树状图法展示所有可能的结果求出n,再从中选出符合事件A或B的结果数目m,求出概率.

练习册系列答案
相关题目
14. 如图,正方形ABCD和正方形DEFG的顶点在y轴上,顶点D、F在x轴上,点C在DE边上,反比例函数y=$\frac{k}{x}$(k≠0)的图象经过B,C和边EF的中点M,若S四边形ABCD=8,则正方形DEFG的面积是( )
如图,正方形ABCD和正方形DEFG的顶点在y轴上,顶点D、F在x轴上,点C在DE边上,反比例函数y=$\frac{k}{x}$(k≠0)的图象经过B,C和边EF的中点M,若S四边形ABCD=8,则正方形DEFG的面积是( )
 如图,正方形ABCD和正方形DEFG的顶点在y轴上,顶点D、F在x轴上,点C在DE边上,反比例函数y=$\frac{k}{x}$(k≠0)的图象经过B,C和边EF的中点M,若S四边形ABCD=8,则正方形DEFG的面积是( )
如图,正方形ABCD和正方形DEFG的顶点在y轴上,顶点D、F在x轴上,点C在DE边上,反比例函数y=$\frac{k}{x}$(k≠0)的图象经过B,C和边EF的中点M,若S四边形ABCD=8,则正方形DEFG的面积是( )| A. | $\frac{23}{9}$ | B. | $\frac{128}{9}$ | C. | 16 | D. | $\frac{15}{4}$ |
11.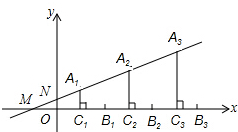 如图,直线y=$\frac{1}{2}$x+1分别与x轴、y轴交于点M,N,一组线段A1C1,A2C2,A3C3,…AnCn的端点A1,A2,A3,…An依次是直线MN上的点,这组线段分别垂直平分线段OB1,B1B2,B2,B3,…,Bn-1Bn,若OB1=B1B2=B2B3=…=Bn-1Bn=4,则点An到x轴的距离为( )
如图,直线y=$\frac{1}{2}$x+1分别与x轴、y轴交于点M,N,一组线段A1C1,A2C2,A3C3,…AnCn的端点A1,A2,A3,…An依次是直线MN上的点,这组线段分别垂直平分线段OB1,B1B2,B2,B3,…,Bn-1Bn,若OB1=B1B2=B2B3=…=Bn-1Bn=4,则点An到x轴的距离为( )
 如图,直线y=$\frac{1}{2}$x+1分别与x轴、y轴交于点M,N,一组线段A1C1,A2C2,A3C3,…AnCn的端点A1,A2,A3,…An依次是直线MN上的点,这组线段分别垂直平分线段OB1,B1B2,B2,B3,…,Bn-1Bn,若OB1=B1B2=B2B3=…=Bn-1Bn=4,则点An到x轴的距离为( )
如图,直线y=$\frac{1}{2}$x+1分别与x轴、y轴交于点M,N,一组线段A1C1,A2C2,A3C3,…AnCn的端点A1,A2,A3,…An依次是直线MN上的点,这组线段分别垂直平分线段OB1,B1B2,B2,B3,…,Bn-1Bn,若OB1=B1B2=B2B3=…=Bn-1Bn=4,则点An到x轴的距离为( )| A. | 4n-4 | B. | 4n-2 | C. | 2n | D. | 2n-2 |
12.2014年1月,Rain时隔四年,发布他第六张专辑《Rain Effect》,Rain为宣传专辑频繁赶通告,Rain所在的公司原计划在2月要Rain出席30个通告,后因新专辑反映热烈,在2月又增加了15个通告,并且比原计划多出席了5天的通告.已知Rain每天出席通告的个数与原计划的相同,求Rain原计划要出席多少天的通告?设Rain原计划要出席x天的通告,根据题意可列正确的方程是( )
| A. | $\frac{30}{x}=\frac{30+15}{x+5}$ | B. | $\frac{30}{x}=\frac{30+15}{x}+5$ | C. | $\frac{30}{x}+5=\frac{30+15}{x}$ | D. | $\frac{30}{x+5}=\frac{30+15}{x}$ |
 如图,AB是⊙O的直径,弦CD与AB相交于点E.
如图,AB是⊙O的直径,弦CD与AB相交于点E.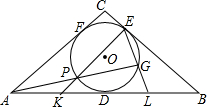 在等腰△ABC中,AC=BC,其内切圆分别与边AB、BC、CA切于点D、E、F.一条过点A且异于AE的直线交△ABC的内切圆于点P、G,EP、EG分别交AB于点K、L.求证:DK=DL.
在等腰△ABC中,AC=BC,其内切圆分别与边AB、BC、CA切于点D、E、F.一条过点A且异于AE的直线交△ABC的内切圆于点P、G,EP、EG分别交AB于点K、L.求证:DK=DL.