题目内容
11.化简:$\frac{x+1}{{x}^{2}-1}$+$\frac{x+1}{x-1}$÷(2-x-$\frac{5x-1}{x-1}$)分析 首先计算括号内的分式的减法,对分式进行化简,然后把除法转化为乘法,然后通分相减即可求解.
解答 解:原式=$\frac{x+1}{(x+1)(x-1)}$+$\frac{x+1}{x-1}$÷$\frac{(2-x)(x-1)-(5x-1)}{x-1}$
=$\frac{1}{x-1}$+$\frac{x}{x-1}$÷$\frac{-{x}^{2}-2x-1}{x-1}$
=$\frac{1}{x-1}$-$\frac{x}{x-1}$•$\frac{x-1}{(x+1)^{2}}$
=$\frac{1}{x-1}$-$\frac{x}{(x+1)^{2}}$
=$\frac{(x+1)^{2}-x(x-1)}{(x-1)(x+1)^{2}}$
=$\frac{3x+1}{(x-1)(x+1)^{2}}$.
点评 本题主要考查分式的混合运算,通分、因式分解和约分是解答的关键.

练习册系列答案
相关题目
1.下列调查中,适合用普查方法的是( )
| A. | 了解某班学生对“五城联创”的知晓率 | |
| B. | 了解某种奶制品中蛋白质的含量 | |
| C. | 了解十堰台《十堰新闻》栏目的收视率 | |
| D. | 了解一批节能灯的使用寿命 |
16.等式2x-y=10变形为-4x+2y=-20的依据为( )
| A. | 等式性质1 | B. | 等式性质2 | C. | 分数的基本性质 | D. | 乘法分配律 |
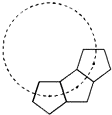 如图,小明将若干个全等的正五边形巧妙地排成环状,则他要完成这一圆环共需10个全等的五边形.
如图,小明将若干个全等的正五边形巧妙地排成环状,则他要完成这一圆环共需10个全等的五边形.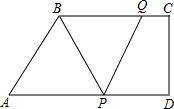 如图,在梯形ABCD中,∠D=90°,BC∥AD.BC=20,DC=16,AD=30,动点P从点D出发,沿射线DA的方向以每秒2个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P、Q分别从点D、C同时出发,当点Q运动到点B时,点P随之停止运动,运动时间为t(秒)
如图,在梯形ABCD中,∠D=90°,BC∥AD.BC=20,DC=16,AD=30,动点P从点D出发,沿射线DA的方向以每秒2个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P、Q分别从点D、C同时出发,当点Q运动到点B时,点P随之停止运动,运动时间为t(秒)