题目内容
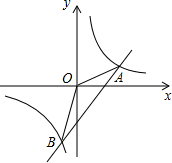 如图,双曲线:y=
如图,双曲线:y=| k |
| x |
(1)求反比例函数和一次函数的解析式;
(2)求△AOB的面积;
(3)根据图象写出一次函数的值大于反比例函数的值的x的取值范围.
考点:反比例函数与一次函数的交点问题
专题:计算题
分析:(1)把A点坐标分别代入y=
(k≠0)和y=x+b中,计算出k和b的值,从而得到反比例函数和一次函数的解析式;
(2)根据反比例函数与一次函数的交点问题,解方程组
得B点坐标(-1,-2),再求出直线y=x-1与y轴的交点C的坐标,然后利用S△AOB=S△AOC+S△BOC进行计算;
(3)观察函数图象,当-1<x<0或x>2时,一次函数的图象都在反比例函数图象的上方.
| k |
| x |
(2)根据反比例函数与一次函数的交点问题,解方程组
|
(3)观察函数图象,当-1<x<0或x>2时,一次函数的图象都在反比例函数图象的上方.
解答: 解:(1)把A(2,1)代入y=
解:(1)把A(2,1)代入y=
得k=2×1=2,
所以反比例函数解析式为y=
;
把A(2,1)代入y=x+b得2+b=1,解得b=-1,
所以一次函数解析式为y=x-1;
(2)解方程组
得
或
,
所以B点坐标为(-1,-2);
当x=0时,y=x-1=-1,则直线y=x-1与y轴的交点C的坐标为(0,-1),
所以S△AOB=S△AOC+S△BOC
=
•1•1+
•1•2
=
;
(3)当-1<x<0或x>2时,一次函数的值大于反比例函数的值.
 解:(1)把A(2,1)代入y=
解:(1)把A(2,1)代入y=| k |
| x |
所以反比例函数解析式为y=
| 2 |
| x |
把A(2,1)代入y=x+b得2+b=1,解得b=-1,
所以一次函数解析式为y=x-1;
(2)解方程组
|
|
|
所以B点坐标为(-1,-2);
当x=0时,y=x-1=-1,则直线y=x-1与y轴的交点C的坐标为(0,-1),
所以S△AOB=S△AOC+S△BOC
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 3 |
| 2 |
(3)当-1<x<0或x>2时,一次函数的值大于反比例函数的值.
点评:本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.也考查了观察函数图象的能力.

练习册系列答案
相关题目
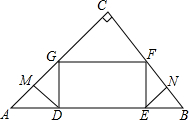 如图,在△ABC中,矩形DEFG的边DE在AB上运动,点F、G分别在BC、AC上,若∠ACB=90°,线段DM、EN分别为∠ADG和∠BEF的角平分线.求证:MG=NF.
如图,在△ABC中,矩形DEFG的边DE在AB上运动,点F、G分别在BC、AC上,若∠ACB=90°,线段DM、EN分别为∠ADG和∠BEF的角平分线.求证:MG=NF.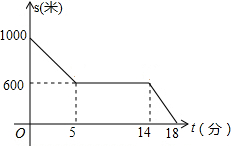 李军下午放学回家,匀速行走,途经新华书店时,他进去买了几本课外书,然后加快速度继续回家.他从学校出发,离家的路程s(米)和离开学校的时间t(分)的关系如图象所示.
李军下午放学回家,匀速行走,途经新华书店时,他进去买了几本课外书,然后加快速度继续回家.他从学校出发,离家的路程s(米)和离开学校的时间t(分)的关系如图象所示. 某印刷厂有甲、乙两种收费方式,除按所印刷数量收取印刷费外,甲种方式还需收取制版费而乙种不需要.两种印刷方式的费用y(元)与印刷份数x(份)之间的函数关系如图所示.
某印刷厂有甲、乙两种收费方式,除按所印刷数量收取印刷费外,甲种方式还需收取制版费而乙种不需要.两种印刷方式的费用y(元)与印刷份数x(份)之间的函数关系如图所示.