题目内容
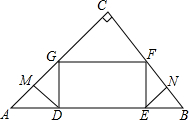 如图,在△ABC中,矩形DEFG的边DE在AB上运动,点F、G分别在BC、AC上,若∠ACB=90°,线段DM、EN分别为∠ADG和∠BEF的角平分线.求证:MG=NF.
如图,在△ABC中,矩形DEFG的边DE在AB上运动,点F、G分别在BC、AC上,若∠ACB=90°,线段DM、EN分别为∠ADG和∠BEF的角平分线.求证:MG=NF.考点:全等三角形的判定与性质
专题:证明题
分析:延长FG,DM交于点H,易证∠HGM=∠NFE和∠H=∠FEN=45°,即可证明△EFN≌△HGM,根据全等三角形对应边相等的性质即可解题.
解答: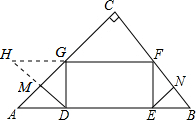 证明:延长FG,DM交于点H,
证明:延长FG,DM交于点H,
∵FG∥AB,
∴∠A=∠HGM,
∵∠A+∠AGD=90°,∠AGD+∠CGF=90°,
∴∠A=∠CGF,
∵∠CGF+∠CFG=90°,∠CFG+∠NFE=90°,
∴∠CGF=∠NFE,
∴∠HGM=∠NFE,
∵DM是∠ADG平分线,EN是∠BEF平分线,
∴∠HDG=∠FEN=45°,
∴HG=DG=EF,∠H=45°,
在△EFN和△HGM中,
,
∴△EFN≌△HGM(ASA),
∴FM=FN.
 证明:延长FG,DM交于点H,
证明:延长FG,DM交于点H,∵FG∥AB,
∴∠A=∠HGM,
∵∠A+∠AGD=90°,∠AGD+∠CGF=90°,
∴∠A=∠CGF,
∵∠CGF+∠CFG=90°,∠CFG+∠NFE=90°,
∴∠CGF=∠NFE,
∴∠HGM=∠NFE,
∵DM是∠ADG平分线,EN是∠BEF平分线,
∴∠HDG=∠FEN=45°,
∴HG=DG=EF,∠H=45°,
在△EFN和△HGM中,
|
∴△EFN≌△HGM(ASA),
∴FM=FN.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△EFN≌△HGM是解题的关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
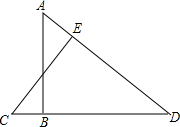 已知:如图,CE⊥AD,垂足为E,∠A=∠C,求证:AB⊥CD.
已知:如图,CE⊥AD,垂足为E,∠A=∠C,求证:AB⊥CD.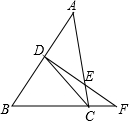 如图,已知CD是直角△ABC斜边上的中线,DF交AC于E,交BC延长线于F,且CD2=DE•DF,求证:
如图,已知CD是直角△ABC斜边上的中线,DF交AC于E,交BC延长线于F,且CD2=DE•DF,求证: 已知CE∥DF,∠ABF=100°,∠CAB=20°,则∠ACE的度数为多少度?
已知CE∥DF,∠ABF=100°,∠CAB=20°,则∠ACE的度数为多少度? 如图,双曲线:
如图,双曲线: