题目内容
20.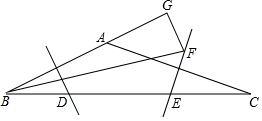 如图,在△ABC中,∠BAC为钝角,边AB、AC的垂直平分线分别交BC于点D、E.
如图,在△ABC中,∠BAC为钝角,边AB、AC的垂直平分线分别交BC于点D、E.(1)若BD2+CE2=DE2,则∠BAC的度数;
(2)若∠ABC的平分线BF和边AC的垂直平分线EF相交于点F,过点F作FG垂直于BA的延长线于点G.求证:BC-AB=2AG.
分析 (1)如图1中,连接AD、AE.首先证明∠DAE=90°,易知∠DBA=∠DAB,∠EAC=∠C,设∠DBA=∠DAB=x,∠EAC=∠C=y,根据三角形内角和定理可得2x+90°+2y=180°,
推出x+y=45°,由此即可解决问题.
(2)如图2中,连接AF,FC,作FM⊥CB于M,只要证明Rt△BFG≌Rt△CFM,Rt△AFG≌Rt△CFM,即可解决问题.
解答 解:(1)如图1中,连接AD、AE.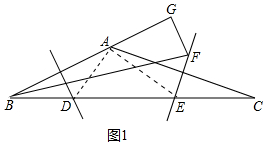
∵边AB、AC的垂直平分线分别交BC于点D、E,
∴BD=DA,EA=EC,
∴∠DBA=∠DAB,∠EAC=∠C,设∠DBA=∠DAB=x,∠EAC=∠C=y,
∵BD2+CE2=DE2,
∴AD2+AE2=DE2,
∴∠DAE=90°,
∴2x+90°+2y=180°,
∴x+y=45°,
∴∠BAC=x+y+90°=135°.
(2)证明:如图2中,连接AF,FC,作FM⊥CB于M,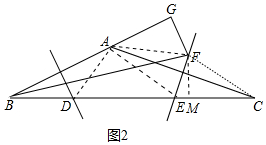
∵BF平分∠CBA,FG⊥BA,FM⊥CB,
∴FG=FM(角平分线上的点到角的两边距离相等),
在Rt△BFG和Rt△BFM中,
$\left\{\begin{array}{l}{BF=BF}\\{FG=FM}\end{array}\right.$
∴Rt△BFG≌Rt△CFM,
∴BG=BM,
∵EF垂直平分线AC,
∴FA=FC(垂直平分线上的点到线段两端点距离相等),
∵FG=FM,∠AFD=∠DMB=90°,
在Rt△AFG和Rt△CFM中,
$\left\{\begin{array}{l}{FG=FM}\\{FA=FC}\end{array}\right.$,
∴Rt△AFG≌Rt△CFM,
∴CM=AG,
∵BC=BM+CM,BG=AB+AG,BG=BM,CM=AG,
∴BC=AB+2AG,
∴BC-AB=2AG.
点评 此题主要考查了全等三角形的判定和性质、线段的垂直平分线的性质、角平分线的性质、勾股定理的逆定理等知识,根据已知角平分线以及垂直平分线作出相关辅助线从而利用全等求出是解决问题的关键.

| A. | 6 | B. | -2 | C. | 6或-2 | D. | 6或-1 |
| A. | 5个 | B. | 8个 | C. | 9个 | D. | 19个 |
| A. | 若a>0,b>0,则a+b>0 | B. | 对顶角相等 | ||
| C. | 全等三角形的对应角相等 | D. | 平行四边形的两组对边分别相等 |
| A. | m=1,n=2 | B. | m=0,n=2 | C. | m=2,n=1 | D. | m=1,n=1 |
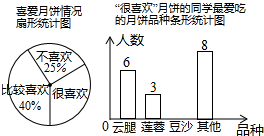 中秋佳节我国有赏月和吃月饼的传统,某校数学兴趣小组为了了解本校学生喜爱月饼的情况,随机抽取了60名同学进行问卷调查,经过统计后绘制了两幅尚不完整的统计图.(注:参与问卷调查的每一位同学在任何一种分类统计中只有一种选择)
中秋佳节我国有赏月和吃月饼的传统,某校数学兴趣小组为了了解本校学生喜爱月饼的情况,随机抽取了60名同学进行问卷调查,经过统计后绘制了两幅尚不完整的统计图.(注:参与问卷调查的每一位同学在任何一种分类统计中只有一种选择)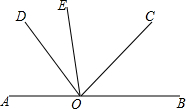 如图,已知,A、O、B在同一条线上,∠AOE=∠COD,∠EOD=30°.
如图,已知,A、O、B在同一条线上,∠AOE=∠COD,∠EOD=30°.