题目内容
3.解不等式组:(1)$\left\{\begin{array}{l}{2x+4≤0}\\{\frac{3}{2}(x+8)-2>0}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{\frac{1}{2}(x+4)<2}\\{\frac{x+3}{3}<\frac{x+2}{2}}\end{array}\right.$.
分析 (1)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集;
(2)与(1)相同作法.
解答 解:(1)解不等式2x+4≤0,得:x≤-2,
解不等式$\frac{3}{2}$(x+8)-2>0,得:x>-$\frac{20}{3}$,
所以不等式组的解集为:-$\frac{20}{3}$<x≤-2;
(2)解不等式$\frac{1}{2}$(x+4)<2,得:x<0,
解不等式$\frac{x+3}{3}<\frac{x+2}{2}$,得:x>0,
所以不等式组无解.
点评 本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
14.抛物线C1:y=x2-4x+8和抛物线C2:y=-x2-8x-18关于点P成中心对称,则点P坐标是( )
| A. | (1,1) | B. | (-1,1) | C. | (-1,-1) | D. | (-3,2) |
 如图,下列条件中:(1)∠B+∠BAD=180°,(2)∠B=∠5,(3)∠3=∠4,(4)∠1=∠2,能判定AD∥BC条件个数有 ( )
如图,下列条件中:(1)∠B+∠BAD=180°,(2)∠B=∠5,(3)∠3=∠4,(4)∠1=∠2,能判定AD∥BC条件个数有 ( )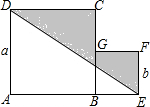 两个边长为a、b的正方形拼成如图所示的形状,连结D、E,求阴影部分的面积.
两个边长为a、b的正方形拼成如图所示的形状,连结D、E,求阴影部分的面积. 如图,AB⊥AC,CD平分∠ACB,BE平分∠ABC,AG∥BC,AG⊥BG.下列结论:①∠BAG=2∠ABF;②BA平分∠CBG;③∠ABG=2∠ACD;④∠ABE=∠ACD,其中正确的结论是( )
如图,AB⊥AC,CD平分∠ACB,BE平分∠ABC,AG∥BC,AG⊥BG.下列结论:①∠BAG=2∠ABF;②BA平分∠CBG;③∠ABG=2∠ACD;④∠ABE=∠ACD,其中正确的结论是( )