题目内容
14.抛物线C1:y=x2-4x+8和抛物线C2:y=-x2-8x-18关于点P成中心对称,则点P坐标是( )| A. | (1,1) | B. | (-1,1) | C. | (-1,-1) | D. | (-3,2) |
分析 求得两个抛物线的顶点坐标,然后求得两顶点连线的中点即可.
解答 解:∵抛物线C1:y=x2-4x+8=(x-2)2+4,
∴顶点(2,4),
∵抛物线C2:y=-x2-8x-18=-(x+4)2-2,
∴顶点为(-4,-2),
∵抛物线C1:y=x2-4x+8和抛物线C2:y=-x2-8x-18关于点P成中心对称,
∴P点的坐标是两个顶点连线的中点,
∴P(-1,1),
故选B.
点评 本题考查了二次函数图象与几何变换,求得抛物线的顶点坐标是解题的关键.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
4.如图图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
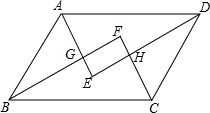 ?ABCD中,AE、CF、BF、DE分别为四个内角平分线,求证:EGFH是矩形.
?ABCD中,AE、CF、BF、DE分别为四个内角平分线,求证:EGFH是矩形. 如图,在两个同心圆中,AB、CD分别是大圆和小圆的直径.求证:四边形ACBD是平行四边形.
如图,在两个同心圆中,AB、CD分别是大圆和小圆的直径.求证:四边形ACBD是平行四边形.