题目内容
5.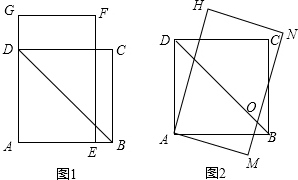 如图1,四边形ABCD是边长为3$\sqrt{2}$的正方形,长方形AEFG的宽AE=$\frac{7}{2}$,长EF=$\frac{7}{2}$$\sqrt{3}$.将长方形AEFG绕点A顺时针旋转15°得到长方形AMNH(如图2),这时BD于MN相交于点O.
如图1,四边形ABCD是边长为3$\sqrt{2}$的正方形,长方形AEFG的宽AE=$\frac{7}{2}$,长EF=$\frac{7}{2}$$\sqrt{3}$.将长方形AEFG绕点A顺时针旋转15°得到长方形AMNH(如图2),这时BD于MN相交于点O.(1)求∠DOM的度数;
(2)在图②中,求点D,N之间的距离.
分析 (1)由旋转的性质,可得∠BAM=15°,即可得∠OKB=∠AOM=75°,又由正方形的性质,可得∠ABD=45°,然后利用外角的性质,即可求得∠DOM的度数;
(2)首先连接AM,交BD于I,连接AN,由特殊角的三角函数值,求得∠HAN=30°,又由旋转的性质,即可求得∠DAN=45°,即可证得A,C,N共线,然后由股定理求得答案.
解答 解:(1)根据题意得:∠BAM=15°,
∵四边形AMNH是矩形,
∴∠M=90°,
∴∠AKM=90°-∠BAM=75°,
∴∠BKO=∠AKM=75°,
∵四边形ABCD是正方形,
∴∠ABD=45°,
∴∠DOM=∠BKO+∠ABD=75°+45°=120°;
(2)连接AN,交BD于I,连接DN,
∵NH=3.5,AH=$\frac{7}{2}\sqrt{3}$,∠H=90°,
∴tan∠HAN=$\frac{NH}{AH}$=$\frac{\sqrt{3}}{3}$,
∴∠HAN=30°,
∴AN=2NH=7,
由旋转的性质:∠DAH=15°,
∴∠DAN=45°,
∵∠DAC=45°,
∴A,C,N共线,
∵四边形ABCD是正方形,
∴BD⊥AC,
∵AD=CD=3$\sqrt{3}$,
∴DI=AI=$\frac{1}{2}$AC=$\frac{1}{2}$$\sqrt{A{B}^{2}+C{D}^{2}}$=3,
∴NI=AN-AI=7-3=4,
在Rt△DIN中,DN=$\sqrt{D{I}^{2}+N{I}^{2}}$=5.
点评 此题考查了旋转的性质、正方形的性质、矩形的性质、勾股定理以及特殊角的三角函数问题.此题难度较大,注意数形结合思想的应用,注意准确作出辅助线是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,△ABC的三个顶点的坐标分别为A(-1,3)、B(-2,-2)、C(4,-2),则△ABC的外接圆圆心的坐标为(1,0),外接圆半径的长度为$\sqrt{13}$.
如图,△ABC的三个顶点的坐标分别为A(-1,3)、B(-2,-2)、C(4,-2),则△ABC的外接圆圆心的坐标为(1,0),外接圆半径的长度为$\sqrt{13}$.
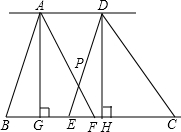 如图,AD∥BC,E,F是BC上的两点,AF,DE相交于点P,四边形EPAB的面积与四边形PFCD的面积相等,则BE=CF,请说明理由.
如图,AD∥BC,E,F是BC上的两点,AF,DE相交于点P,四边形EPAB的面积与四边形PFCD的面积相等,则BE=CF,请说明理由.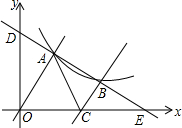 已知直线y=-$\frac{2}{3}$x+6与双曲线y=$\frac{k}{x}$(x>0)交于点A、B,把直线OA向右平移恰好经过点B,并与x轴交于点C,且OA:BC=2:1
已知直线y=-$\frac{2}{3}$x+6与双曲线y=$\frac{k}{x}$(x>0)交于点A、B,把直线OA向右平移恰好经过点B,并与x轴交于点C,且OA:BC=2:1