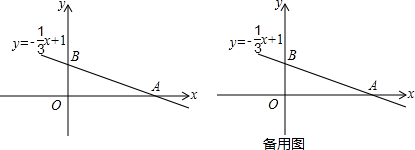
题目内容
6．在等边△ABC中，AD是∠BAC的角平分线，则$\frac{AD}{AC}$=$\frac{\sqrt{3}}{2}$．分析 由等边三角形的性质得出∠C=60°，∠ADC=90°，由三角函数即可得出结果．
解答 解：如图所示：
∵△ABC是等边三角形，
∴∠C=60°，
∵AD是∠BAC的角平分线，
∴AD⊥BC，
∴∠ADC=90°，
在Rt△ACD中，sinC=$\frac{AD}{AC}$，
∴$\frac{AD}{AC}$=sin60°=$\frac{\sqrt{3}}{2}$；
故答案为：$\frac{\sqrt{3}}{2}$．
点评 本题考查了等边三角形的性质、三角函数；熟练掌握等边三角形的性质，并能进行推理计算是解决问题的关键．
练习册系列答案
英语小英雄天天默写系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
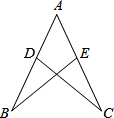如图，已知AB=AC，∠B=∠C，求证：△ABE≌△ACD．
如图，点P在反比例函数y=$\frac{k}{x}$的图象上，且PD⊥x轴于点D．若△POD的面积为3，则k的值是-6．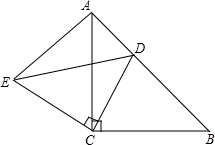
如图所示，已知△ABC和△ECD都是等腰直角三角形，∠ACB=∠DCE=90．D为AB边上-点，若AB=10cm，AD=3cm，求AE的长．
如图，AD=BC，BD=AC，求证：AB∥CD．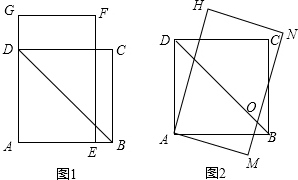
如图1，四边形ABCD是边长为3$\sqrt{2}$的正方形，长方形AEFG的宽AE=$\frac{7}{2}$，长EF=$\frac{7}{2}$$\sqrt{3}$．将长方形AEFG绕点A顺时针旋转15°得到长方形AMNH（如图2），这时BD于MN相交于点O．