题目内容
15.解方程组:$\left\{\begin{array}{l}{2x+y+3z=11}\\{3x+2y-2z=11}\\{4x-3y-2z=4}\end{array}\right.$.分析 对于$\left\{\begin{array}{l}{2x+y+3z=11①}\\{3x+2y-2z=11②}\\{4x-3y-2z=4③}\end{array}\right.$,利用①×2+②×3得13x+8y=55,利用③-②得x-5y=-7,再解关于x和y的二元一次方程组,然后利用代入法求出z,从而得到原方程组的解.
解答 解:$\left\{\begin{array}{l}{2x+y+3z=11①}\\{3x+2y-2z=11②}\\{4x-3y-2z=4③}\end{array}\right.$,
①×2+②×3得13x+8y=55④,
③-②得x-5y=-7⑤,
由④⑤组成方程组$\left\{\begin{array}{l}{13x+8y=55}\\{x-5y=-7}\end{array}\right.$得$\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$,
把x=3,y=2代入①得6+2+3z=11,
解得z=1.
所以原方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=2}\\{z=1}\end{array}\right.$.
点评 本题考查了三元一次方程组:利用加减消元法或代入消元法把解三元一次方程组的问题转化为解二元一次方程组的问题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
4.下个各式成立的是( )
| A. | $\sqrt{(-2)^{2}}$=-2 | B. | $\sqrt{(-5)^{2}}$=-5 | C. | $\sqrt{(-6)^{2}}$=6 | D. | $\sqrt{{x}^{2}}$=x |
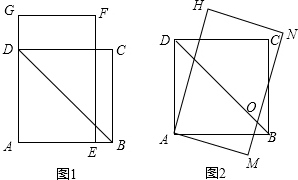 如图1,四边形ABCD是边长为3$\sqrt{2}$的正方形,长方形AEFG的宽AE=$\frac{7}{2}$,长EF=$\frac{7}{2}$$\sqrt{3}$.将长方形AEFG绕点A顺时针旋转15°得到长方形AMNH(如图2),这时BD于MN相交于点O.
如图1,四边形ABCD是边长为3$\sqrt{2}$的正方形,长方形AEFG的宽AE=$\frac{7}{2}$,长EF=$\frac{7}{2}$$\sqrt{3}$.将长方形AEFG绕点A顺时针旋转15°得到长方形AMNH(如图2),这时BD于MN相交于点O. 如图,在?ABCD中,E、F在平行四边形的外部,且AE=CF,BE=DF,试指出AC和EF的关系,并说明理由.
如图,在?ABCD中,E、F在平行四边形的外部,且AE=CF,BE=DF,试指出AC和EF的关系,并说明理由. 在△ABC中,∠B=∠C,点D、E分别在BC、AC上,AD=AE,试猜想∠BAD和∠EDC有何数量关系?并说明理由.
在△ABC中,∠B=∠C,点D、E分别在BC、AC上,AD=AE,试猜想∠BAD和∠EDC有何数量关系?并说明理由.