题目内容
17．
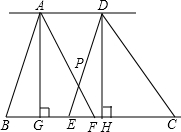如图，AD∥BC，E，F是BC上的两点，AF，DE相交于点P，四边形EPAB的面积与四边形PFCD的面积相等，则BE=CF，请说明理由．
分析 由四边形EPAB的面积与四边形PFCD的面积相等，得到S△ABF=S△DEC，于是得到$\frac{1}{2}$BF•AG=$\frac{1}{2}$CE•DH，根据AD∥BC，推出AG=DH，得到BF=CE，然后根据线段的和差即可得到距离．
解答 解：∵四边形EPAB的面积与四边形PFCD的面积相等，
∴S△ABF=S四边形ABEP+S△PEF=S四边形PFCD+S△PEF=S△DEC，
∴$\frac{1}{2}$BF•AG=$\frac{1}{2}$CE•DH，
∵AD∥BC，
∴AG=DH，
∴BF=CE，
∴BF-EF=CE-EF，
即BE=CF．
点评 本题考查了平行线间的距离，三角形的面积，熟记平行线间的距离相等是解题的关键．
练习册系列答案
相关题目
20．计算：1-2所得的正确结果是（ ）
| A． | -1 | B． | -3 | C． | 1 | D． | 3 |
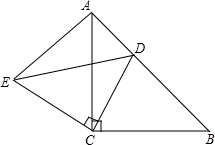如图所示，已知△ABC和△ECD都是等腰直角三角形，∠ACB=∠DCE=90．D为AB边上-点，若AB=10cm，AD=3cm，求AE的长．
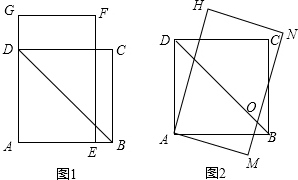如图1，四边形ABCD是边长为3$\sqrt{2}$的正方形，长方形AEFG的宽AE=$\frac{7}{2}$，长EF=$\frac{7}{2}$$\sqrt{3}$．将长方形AEFG绕点A顺时针旋转15°得到长方形AMNH（如图2），这时BD于MN相交于点O．
如图，在?ABCD中，E、F在平行四边形的外部，且AE=CF，BE=DF，试指出AC和EF的关系，并说明理由．