题目内容
8. 如图,△ABC的三个顶点的坐标分别为A(-1,3)、B(-2,-2)、C(4,-2),则△ABC的外接圆圆心的坐标为(1,0),外接圆半径的长度为$\sqrt{13}$.
如图,△ABC的三个顶点的坐标分别为A(-1,3)、B(-2,-2)、C(4,-2),则△ABC的外接圆圆心的坐标为(1,0),外接圆半径的长度为$\sqrt{13}$.
分析 根据三角形的外心是三边中垂线的交点,由B、C的坐标可知,圆心M必在直线x=1上;由图知:AC的垂直平分线正好经过(1,0),由此可得到M(1,0);连接MB,过M作MD⊥BC于D,由勾股定理即可求得⊙M的半径长.
解答 解:设△ABC的外心为M;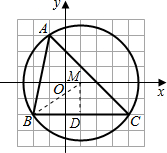
∵B(-2,-2),C(4,-2),
∴M必在直线x=1上,
由图知:AC的垂直平分线过(1,0),
故M(1,0);
过M作MD⊥BC于D,连接MB,
Rt△MBD中,MD=2,BD=3,
由勾股定理得:MB=$\sqrt{M{D}^{2}+B{D}^{2}}$=$\sqrt{13}$,
即△ABC的外接圆半径为$\sqrt{13}$.
故答案为:(1,0);$\sqrt{13}$.
点评 本题考查的是三角形的外接圆和外心的概念和性质,掌握三角形的外心是三边中垂线的交点、确定圆心的位置是解题的关键.

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
20.计算:1-2所得的正确结果是( )
| A. | -1 | B. | -3 | C. | 1 | D. | 3 |
 如图,奥运福娃在5×5的方格(每小格边长为1m)上沿着网格线运动,贝贝从A处出发去寻找B、C、D处的其它福娃,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+3),从B到A记为:B→A(-1,-3),其中第一个数表示左右方向,第二个数表示上下方向,那么图中
如图,奥运福娃在5×5的方格(每小格边长为1m)上沿着网格线运动,贝贝从A处出发去寻找B、C、D处的其它福娃,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+3),从B到A记为:B→A(-1,-3),其中第一个数表示左右方向,第二个数表示上下方向,那么图中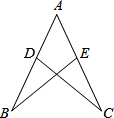 如图,已知AB=AC,∠B=∠C,求证:△ABE≌△ACD.
如图,已知AB=AC,∠B=∠C,求证:△ABE≌△ACD.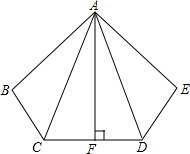 如图,已知AF⊥CD于点F,AC=AD,∠BCD=∠EDC,BC=DE.
如图,已知AF⊥CD于点F,AC=AD,∠BCD=∠EDC,BC=DE. 请确定一个点P,使得点P到AB和BC的距离相等,且满足它到点A和点C的距离相等.(不写作法,保留作图痕迹.)
请确定一个点P,使得点P到AB和BC的距离相等,且满足它到点A和点C的距离相等.(不写作法,保留作图痕迹.) 如图,点P在反比例函数y=$\frac{k}{x}$的图象上,且PD⊥x轴于点D.若△POD的面积为3,则k的值是-6.
如图,点P在反比例函数y=$\frac{k}{x}$的图象上,且PD⊥x轴于点D.若△POD的面积为3,则k的值是-6.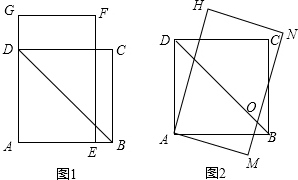 如图1,四边形ABCD是边长为3$\sqrt{2}$的正方形,长方形AEFG的宽AE=$\frac{7}{2}$,长EF=$\frac{7}{2}$$\sqrt{3}$.将长方形AEFG绕点A顺时针旋转15°得到长方形AMNH(如图2),这时BD于MN相交于点O.
如图1,四边形ABCD是边长为3$\sqrt{2}$的正方形,长方形AEFG的宽AE=$\frac{7}{2}$,长EF=$\frac{7}{2}$$\sqrt{3}$.将长方形AEFG绕点A顺时针旋转15°得到长方形AMNH(如图2),这时BD于MN相交于点O.