Question

20．如图1，在锐角△ABC中，AD⊥BC于D，BE⊥AC于E，AD与BE相交于F，且BF=AC．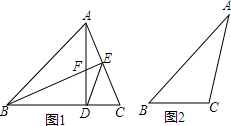
（1）求证：ED平分∠FEC；
（2）如图2，若△ABC中，∠C为钝角，其他条件不变，（1）中结论是否仍成立？自己画图，并证明你的结论．

Answer 1

分析 （1）求出∠DBF=∠DAC，由AAS证明△BDF≌△ADC．得出对应边相等BD=AD，由等腰直角三角形的性质得出∠BAD=∠ABD=45°，证明A、B、D、E四点共圆，由圆周角定理得出∠BED=∠BAD=45°，得出∠CED=∠BED，即可得出结论；
（2）同（1）由AAS证明△BDF≌△ADC，得出BD=AD，由等腰直角三角形的性质得出∠BAD=∠ABD=45°，证明A、B、E、D四点共圆，由圆周角定理得出∠DEA=∠ABD=45°，得出∠DEF=∠DEA，即可得出结论．

解答 （1）证明：∵AD⊥BC，BE⊥AC，
∴∠BDF=∠ADC=90°，∠AEB=∠FEC=90°，
∵∠DBF+∠C=90°，∠DAC+∠C=90°，
∴∠DBF=∠DAC，
在△BDF和△ADC中，
$\left\{\begin{array}{l}{∠BDF=∠ADC}&{\;}\\{∠DBF=∠DAC}&{\;}\\{BF=AC}&{\;}\end{array}\right.$，
∴△BDF≌△ADC（AAS），
∴BD=AD，
∴∠BAD=∠ABD=45°，
∵∠AEB=∠ADB=90°，
∴A、B、D、E四点共圆，
∴∠BED=∠BAD=45°，
∴∠CED=90°-45°=45°=∠BED，
∴ED平分∠FEC；
（2）解：（1）中结论成立；理由如下：如图所示：
∵AD⊥BC，BE⊥AC，
∴∠BDF=∠ADC=90°，∠AEB=∠FEC=90°，
∵∠DBF+∠F=90°，∠DAC+∠F=90°，
∴∠DBF=∠DAC，
在△BDF和△ADC中，
$\left\{\begin{array}{l}{∠BDF=∠ADC}&{\;}\\{∠DBF=∠DAC}&{\;}\\{BF=AC}&{\;}\end{array}\right.$．
∴△BDF≌△ADC（AAS），
∴BD=AD，
∴∠BAD=∠ABD=45°，
∵∠AEB=∠ADB=90°，
∴A、B、E、D四点共圆，
∴∠DEA=∠ABD=45°，
∴∠DEF=90°-∠DEA=45°=∠DEA，
∴ED平分∠FEC．

点评 本题考查了全等三角形的判定与性质、等腰直角三角形的判定与性质、四点共圆、圆周角定理、直角三角形的性质等知识；本题综合性强，有一定难度，证明三角形全等和四点共圆是解决问题的关键．