题目内容
3．若函数y=2x2-8x+m的图象上有两点A（x1，y1），B（x2，y2），若x1＜x2＜-2，则（ ）| A． | y1＜y2 | B． | y1＞y2 | ||
| C． | y1=y2 | D． | y1、y2、的大小不确定 |
分析 根据配方法把二次函数的一般式化为顶点式，求出抛物线的对称轴，根据二次函数的性质判断即可．
解答 解：y=2x2-8x+m=2（x-2）2+m-8，
则抛物线开口向上，对称轴是x=2，
∴当x＜2时，y随x的增大而减小，
∴x1＜x2＜-2时，y1＞y2，
故选：B．
点评 本题考查二次函数图象上点的坐标特征、函数的增减性等知识，解题的关键是灵活运用二次函数的性质．
练习册系列答案
相关题目
13．
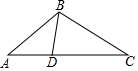如图，△ABC中，点D在AC边上，添加下列条件后仍不能判别△ABD∽△ACB的是（ ）
如图，△ABC中，点D在AC边上，添加下列条件后仍不能判别△ABD∽△ACB的是（ ）| A． | ∠ABD=∠C | B． | ∠ADB=∠ABC | C． | $\frac{AD}{AB}$=$\frac{AB}{AC}$ | D． | $\frac{AD}{AB}$=$\frac{BD}{BC}$ |
如图，△ABC中，AB=AC
11．
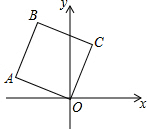如图，在正方形OABC中，点A的坐标是（-3，1），点B的纵坐标是4，则B，C两点的坐标分别是（ ）
如图，在正方形OABC中，点A的坐标是（-3，1），点B的纵坐标是4，则B，C两点的坐标分别是（ ）| A． | （-2，4），（1，3） | B． | （-2，4），（2，3） | C． | （-3，4），（1，4） | D． | （-3，4），（1，3） |
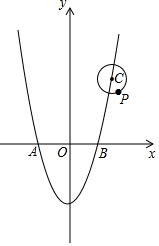【材料阅读】阅读下列一段文字，然后回答下列问题．
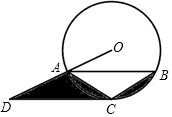如图，△ABC内接于⊙O，CA=CB，CD∥AB且与OA的延长线交于点D．