题目内容
在一个口袋中,共有50个球,其中白球20个,红球20个,其余为篮球,从中任摸一球,摸到不是白球的概率是( )
A. 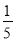 B.
B. 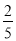 C.
C. 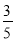 D.
D. 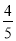
 C
【解析】口袋中,共有50个球,其中白球20个,那么不是白球的球共有30个,所以摸到不是白球的概率是,故选C.
C
【解析】口袋中,共有50个球,其中白球20个,那么不是白球的球共有30个,所以摸到不是白球的概率是,故选C.
练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案
相关题目
如果(2x+m)(x-5)展开后的结果中不含x的一次项,那么m等于( )
A. 5 B. -10 C. -5 D. 10
 D
【解析】(2x+m)(x-5)=2x2+mx-10x-5m,因展开后的结果中不含x的一次项,可得m-10=0,解得m=10,故选D.
D
【解析】(2x+m)(x-5)=2x2+mx-10x-5m,因展开后的结果中不含x的一次项,可得m-10=0,解得m=10,故选D. 观察下列运算并填空.
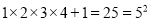 ;
;
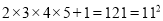 ;
;
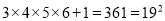 ;
; 
根据以上结果,猜想并研究: 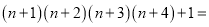 __________.
__________.
 【解析】试题解析:
…
故答案为: .
【解析】试题解析:
…
故答案为: . 下面是两个可以自由转动的转盘,转动转盘,分别计算转盘停止后,指针落在红色区域的概率.
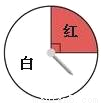
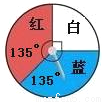
 【解析】分析:本题考察对概率意义的理解,关键是根据图示,由圆心角的度数求出概率.
本题解析:
由图可以看出,在第一个转盘内,红色区域的圆心角是90°,因此可以算得指针落在红色区域的概率是;在第二个转盘内,红色区域的圆心角是135°,因此可以算得指针落在红色区域的概率是 .
【解析】分析:本题考察对概率意义的理解,关键是根据图示,由圆心角的度数求出概率.
本题解析:
由图可以看出,在第一个转盘内,红色区域的圆心角是90°,因此可以算得指针落在红色区域的概率是;在第二个转盘内,红色区域的圆心角是135°,因此可以算得指针落在红色区域的概率是 . 向如图所示的正三角形区域扔沙包(区域中每一个小正三角形除颜色外完全相同),假设沙包击中每一个小三角形是等可能的,扔沙包1次击中阴影区域的概率等于_______.
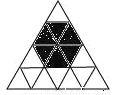
 【解析】由图可以看出,一共有最小规格的正三角形16个,其中涂黑了的有6个.有等可能的情况之下,扔沙包1次击中阴影区域的概率等于.故答案为: .
【解析】由图可以看出,一共有最小规格的正三角形16个,其中涂黑了的有6个.有等可能的情况之下,扔沙包1次击中阴影区域的概率等于.故答案为: . 从1至9这些数字中任意取一个,取出的数字是偶数的概率是( )
A. 0 B. 1 C. 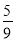 D.
D. 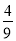
 D
【解析】在1至9这些数字中,共有2,4,6,8四个偶数,因此从这九个数字中任意取一个,取出的数字是偶数的概率是.故选D.
D
【解析】在1至9这些数字中,共有2,4,6,8四个偶数,因此从这九个数字中任意取一个,取出的数字是偶数的概率是.故选D. 如图所示,小明在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1: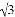 ,点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.
,点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.
(1)山坡坡角(即∠ABC)的度数等于_____度;
(2)求山坡A、B两点间的距离(结果精确到0.1米).
(参考数据: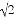 ≈1.414,
≈1.414,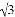 ≈1.732)
≈1.732)
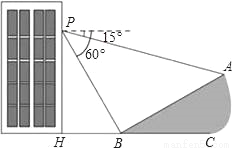
 30 (2) 34.6米
【解析】试题分析:(1)根据俯角以及坡度的定义即可求解;
(2)在直角△PHB中,根据三角函数即可求得PB的长,然后在直角△PBA中利用三角函数即可求解.
试题解析:(1)∵山坡的坡度i(即tan∠ABC)为1:.
∴tan∠ABC=,∴∠ABC=30°;∵从P点望山脚B处的俯角60°,
∴∠PBH=60°,∴∠ABP=180°﹣30°﹣60...
30 (2) 34.6米
【解析】试题分析:(1)根据俯角以及坡度的定义即可求解;
(2)在直角△PHB中,根据三角函数即可求得PB的长,然后在直角△PBA中利用三角函数即可求解.
试题解析:(1)∵山坡的坡度i(即tan∠ABC)为1:.
∴tan∠ABC=,∴∠ABC=30°;∵从P点望山脚B处的俯角60°,
∴∠PBH=60°,∴∠ABP=180°﹣30°﹣60... 在Rt△ABC中,∠C=90°,cosB=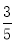 ,AB=10cm,则BC的长度为( )
,AB=10cm,则BC的长度为( )
A. 6cm B. 7cm
C. 8cm D. 9cm
 A
【解析】
试题分析:根据cosB=0.6可得:,则BC=6cm.
A
【解析】
试题分析:根据cosB=0.6可得:,则BC=6cm. 如图,把大小为4×4的正方形方格分割成两个全等图形,例如图1,请在下图中,沿着虚线画出四种不同的分法,把4×4的正方形方格分割成两个全等图形.

 见解析
【解析】试题分析:可以利用图形的对称性和互补性来分隔成两个全等的图形.
试题解析:∵要求分成全等的两块,
∴每块图形要包含有8个小正方形.
见解析
【解析】试题分析:可以利用图形的对称性和互补性来分隔成两个全等的图形.
试题解析:∵要求分成全等的两块,
∴每块图形要包含有8个小正方形. 
