题目内容
6.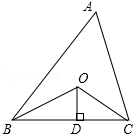 如图,已知△ABC的面积是20,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,则△ABC的周长是$\frac{40}{3}$.
如图,已知△ABC的面积是20,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,则△ABC的周长是$\frac{40}{3}$.
分析 根据角平分线上的点到角的两边的距离相等可得点O到AB、AC、BC的距离都相等,从而可得到△ABC的面积等于周长的一半乘以OD,然后列式进行计算即可求解.
解答 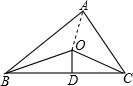 解:如图,连接OA,
解:如图,连接OA,
∵OB、OC分别平分∠ABC和∠ACB,
∴点O到AB、AC、BC的距离都相等,
∵△ABC的面积是20,OD⊥BC于D,且OD=3,
∴S△ABC=$\frac{1}{2}$×(AB+BC+AC)×3=20.
∴AB+BC+AC=$\frac{40}{3}$,
故答案为:$\frac{40}{3}$.
点评 本题考查了角平分线上的点到角的两边的距离相等的性质,判断出三角形的面积与周长的关系是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.已知△ABC~△DEF,相似比为3:1,且△ABC的面积与△DEF的面积和为20,则△DEF的面积为( )
| A. | 5 | B. | 2 | C. | 15 | D. | 18 |
15.如图,已知△ABC,则甲、乙、丙三个三角形中和△ABC全等的是( )
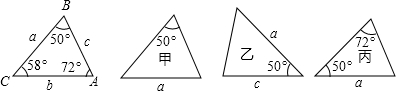

| A. | 只有乙 | B. | 只有丙 | C. | 甲和乙 | D. | 乙和丙 |
 已知二次函数y=x2+2x+$\frac{k-1}{2}$与x轴有两个交点,且k为正整数.
已知二次函数y=x2+2x+$\frac{k-1}{2}$与x轴有两个交点,且k为正整数.