题目内容
5. 已知二次函数y=x2+2x+$\frac{k-1}{2}$与x轴有两个交点,且k为正整数.
已知二次函数y=x2+2x+$\frac{k-1}{2}$与x轴有两个交点,且k为正整数.(1)求k的值;
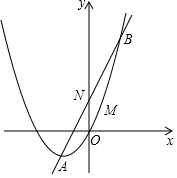
(2)当二次函数y=x2+2x+$\frac{k-1}{2}$图象经过原点时,直线y=3x+2与之交于A、B两点,若M是抛物线上在直线y=3x+2下方的一个动点,△MAB面积是否存在最大值?若存在,请求出M点坐标,并求出△MAB面积最大值;若不存在,请说明理由.
(3)将(2)中的二次函数图象x轴下方的部分沿x轴翻折到x轴上方,图象的其余部分保持不变,翻折后的图象与原图象x轴上方的部分组成一个新图象.若直线y=kx+2(k>0)与该新图象恰好有三个公共点,求k的值.
分析 (1)一元二次方程根的判别式即可确定出k的值;
(2)先判断出平行于直线y=3x+2的直线与抛物线只有一个交点时,△MAB的面积最大,再求出点M的坐标,再用三角形的面积公式;
(3)找出直线y=kx+2与新图象恰有三个交点时的分界位置,分别求出即可.
解答 解:(1)∵二次函数y=x2+2x+$\frac{k-1}{2}$与x轴有两个交点,
∴△=b2-4ac=4-4×$\frac{k-1}{2}$>0,
∴k-1<2.
∴k<3.
∵k为正整数,
∴k为1,2.
(2)如图1, 把x=0代入方程x2+2x+$\frac{k-1}{2}$=0中,得k=1,
把x=0代入方程x2+2x+$\frac{k-1}{2}$=0中,得k=1,
此时二次函数为y=x2+2x,
此时直线y=3x+2与二次函数y=x2+2x的交点为A(-1,-1),B(2,8)
设与直线y=3x+2平行的直线为y=3x+b,列方程组得:$\left\{\begin{array}{l}{y={x}^{2}+2x}\\{y=3x+b}\end{array}\right.$
即:x2-x-b=0,
∴△=b2-4ac=1+4b=0,
∴b=-$\frac{1}{4}$时有一个交点,代入x2-x-b=0中,
得交点M坐标为($\frac{1}{2}$,$\frac{5}{4}$),
过点M作MN∥x轴交直线AB于点N,点N坐标为(-$\frac{1}{4}$,$\frac{5}{4}$).∴MN=$\frac{3}{4}$.
∴S△MAB=$\frac{1}{2}$MN(yB-yA)=$\frac{1}{2}×\frac{3}{4}×9=\frac{27}{8}$.
(3)由于新图象的封闭部分与原图象的封闭部分关于x轴对称,所以其解析式为y=-x2-2x,
当直线与新图象有3个公共点(如图2所示) ,直线为l1、l2,其中l1过点C,l2与翻转部分图象有一个交点.分为以下两种情况:
,直线为l1、l2,其中l1过点C,l2与翻转部分图象有一个交点.分为以下两种情况:
①直线l1:y=kx+2过点C(-2,0),代入y=kx+2得:k=1.
②直线l2:
则$\left\{\begin{array}{l}{y=kx+2}\\{y=-{x}^{2}-2x}\end{array}\right.$有一组解,此时x2+2x+kx+2有两个相等的实数根,
即△=0,解得:k=-2+2$\sqrt{2}$或k=-2-2$\sqrt{2}$.
综上所述k=1或k=-2+2$\sqrt{2}$时,与该新图象恰好有三个公共点.
点评 此题是二次函数综合题,主要考查了一元二次方程根的判别式,解方程组,极值的确定,解(2)的关键是判断出△MAB的面积最大时点M的位置,解(3)直线y=kx+2与新图象有三个交点时的位置,是一道比较好的中考常考题.

 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案| A. | a4•a5=a20 | B. | x8÷x2=x4 | C. | (a3)2=a9 | D. | (3a2)2=9a4 |
| A. | $\sqrt{24}$ | B. | $\sqrt{36}$ | C. | $\sqrt{11}$ | D. | $\sqrt{20}$ |
| A. | BC=EF | B. | ∠A=∠D | C. | AC=DF | D. | ∠C=∠F |
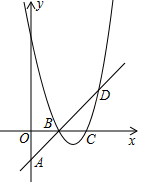 已知抛物线y=ax2+bx+8(a≥1)过点D(5,3),与x轴交于点B、C(点B、C均在y轴右侧)且BC=2,直线BD交y轴于点A.
已知抛物线y=ax2+bx+8(a≥1)过点D(5,3),与x轴交于点B、C(点B、C均在y轴右侧)且BC=2,直线BD交y轴于点A.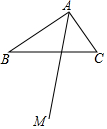 如图,在Rt△ABC中,∠BAC=90°,AB>AC,射线AM平分∠BAC.
如图,在Rt△ABC中,∠BAC=90°,AB>AC,射线AM平分∠BAC.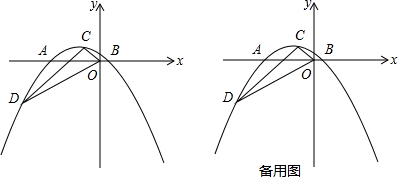
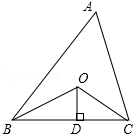 如图,已知△ABC的面积是20,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,则△ABC的周长是$\frac{40}{3}$.
如图,已知△ABC的面积是20,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,则△ABC的周长是$\frac{40}{3}$.


