已知.函数y=ax2+x-1的图象与x轴只有一个公共点(1)求这个函数关系式,(2)如图1.平行于x轴的直线交抛物线于E.F两点.若以线段EF为直径的圆M经过点B.求线段MA的长,(3)如图2.设二次函数y=ax2+x-1图象的顶点为B.与y轴的交点为A.P为图象上的一点.若以线段PB为直径的圆与直线AB相切于点B.求P点的坐标,中.若圆与x轴另一交点点关于直线P 题目和参考答案——青夏教育精英家教网—

题目内容

已知，函数y=ax²+x-1（a≠0）的图象与x轴只有一个公共点
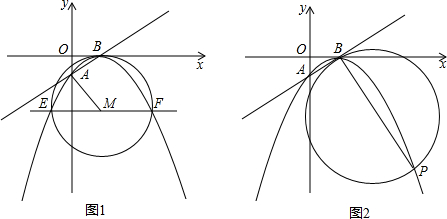
（1）求这个函数关系式；
（2）如图1，平行于x轴的直线交抛物线于E、F两点，若以线段EF为直径的圆M经过点B，求线段MA的长；
（3）如图2，设二次函数y=ax²+x-1图象的顶点为B，与y轴的交点为A，P为图象上的一点，若以线段PB为直径的圆与直线AB相切于点B，求P点的坐标；
（4）在（3）中，若圆与x轴另一交点点关于直线PB的对称点为D，试探索点D是否在抛物线y=ax²-x-1上，若在抛物线上，求出D点的坐标；若不在，请说明理由．

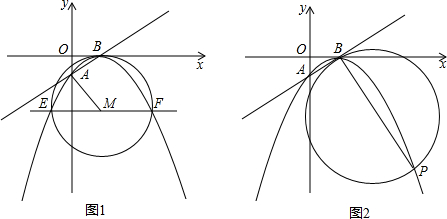
考点：二次函数综合题

专题：

分析：（1）a≠0，此函数是二次函数，可由根的判别式求出a的值，以此确定其解析式；
（2）由抛物线对称轴为x=2，设满足条件的圆的半径为R，点E在对称轴左侧，则E的坐标为（2-R，-R），而E点在抛物线y=-

x²+x-1上，代入解析式中求出R即可解决问题；
（3）设圆与x轴的另一个交点为C，连接PC，由圆周角定理知PC⊥BC；由于PB是圆的直径，且AB切圆于B，得PB⊥AB，由此可证得△PBC∽△BAO，根据两个相似三角形的对应直角边成比例，即可得到PC、BC的比例关系，可根据这个比例关系来设P点的坐标，联立抛物线的解析式即可求出P点的坐标；
（4）连接CM，设CM与PB的交点为Q，由于C、M关于直线PB对称，那么PB垂直平分CM，即CQ=QM；过M作MD⊥x轴于D，取CD的中点E，连接QE，则QE是Rt△CMD的中位线；在Rt△PCB中，CQ⊥OB，QE⊥BC，易证得∠BQE、∠QCE都和∠CPQ相等，因此它们的正切值都等于

（在（2）题已经求得）；由此可得到CE=2QE=4BE，（2）中已经求出了CB的长，根据CE、BE的比例关系，即可求出BE、CE、QE的长，由此可得到Q点坐标，也就得到M点的坐标，然后将点M代入抛物线的解析式中进行判断即可．

解答：

解：（1）当a≠0时，△=1+4a=0，a=-

，此时，图象与x轴只有一个公共点．
∴函数的解析式为：y=-

x²+x-1；

（2）由（1）知，抛物线的解析式为y=-

x²+x-1．
则y=-

x²+x-1=-

（x-2）²．点A的坐标是（0，-1）．
∵以线段EF为直径的圆M经过点B，EF∥x轴，
∴点B为抛物线的顶点，
故设⊙M的半径为R，则E的坐标为（2-R，-R），将其代入y=-

（x-2）²，得
-R=-

（2-R-2）²
解得 R=4．
∴点M的坐标是（2，-4）．
∴MA=

22+(-4+1)2

；

（3）设P为二次函数图象上的一点，过点P作PC⊥x轴于点C；
∵y=ax²+x-1是二次函数，由（1）知该函数关系式为：
y=-

x²+x-1，
∴顶点为B（2，0），图象与y轴的交点坐标为A（0，-1）
∵以PB为直径的圆与直线AB相切于点B
∴PB⊥AB则∠PBC=∠BAO
∴Rt△PCB∽Rt△BOA
∴

，故PC=2BC，
设P点的坐标为（x，y），
∵∠ABO是锐角，∠PBA是直角，
∴∠PBO是钝角，
∴x＞2
∴BC=x-2，PC=2x-4，
即y=4-2x，P点的坐标为（x，4-2x）
∵点P在二次函数y=-

x²+x-1的图象上，
∴4-2x=-

x²+x-1
解得：x₁=10，x₂=2
∴P点的坐标为：（10，-16）

（3）点M不在抛物线y=ax²+x+1上
由（2）知：C为圆与x轴的另一交点，连接CM，CM与直线PB的交点为Q，过点M作x轴的垂线，垂足为D，取CD的中点E，连接QE，则CM⊥PB，且CQ=MQ，即QE是中位线．
∴QE∥MD，QE=

MD，QE⊥CE
∵CM⊥PB，QE⊥CE，PC⊥x轴
∴∠QCE=∠EQB=∠CPB
∴tan∠QCE=tan∠EQB=tan∠CPB=

CE=2QE=2×2BE=4BE，又CB=8，
故BE=

，QE=

，
∴Q点的坐标为（-

，

）
可求得M点的坐标为（

，

）
∵

×（

）²+

-1=

≠