题目内容
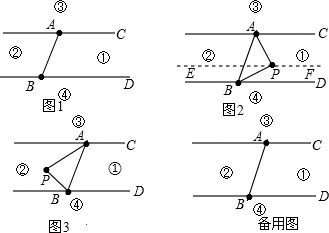
如图1,直线AC、BD及线段AB把平面分成①、②、③、④四个部分(规定:线上各点不属于任何部分).当动点P落在某个部分时,连接PA,PB,可得到∠PAC,∠APB,∠PBD三个角.(提示:有公共端点的两条重合的射线所组成的角是0°)
(1)如图2,当动点P落在第①部分时,如果∠APB=∠PAC+∠PBD,那么AC与BD平行吗?请说明理由;
(2)当动点P落在第②部分时,∠PAC、∠APB、∠PBD三个角满足什么等量关系时,AC与BD平行(不需说明理由);
(3)如果直线AC∥BD,探究动点P在什么区域时,存在∠APB=∠PBD-∠PAC,请在图3中用阴影表示出动点P所在区域.
(1)如图2,当动点P落在第①部分时,如果∠APB=∠PAC+∠PBD,那么AC与BD平行吗?请说明理由;
(2)当动点P落在第②部分时,∠PAC、∠APB、∠PBD三个角满足什么等量关系时,AC与BD平行(不需说明理由);
(3)如果直线AC∥BD,探究动点P在什么区域时,存在∠APB=∠PBD-∠PAC,请在图3中用阴影表示出动点P所在区域.

考点:平行线的判定与性质
专题:
分析:(1)过P作PQ∥AC,结合平行线的性质及已知条件可得到∠BPQ=∠PBD,可判定PQ∥BD,结合平行的传递性可证明AC∥BD;
(2)类似(1)的方法,可得出结论;
(3)利用三角形外角的性质和平行线的性质可得出点P在的区域.
(2)类似(1)的方法,可得出结论;
(3)利用三角形外角的性质和平行线的性质可得出点P在的区域.
解答:
解:
(1)AC∥BD,
理由如下:过点P作PQ∥AC,如图2,
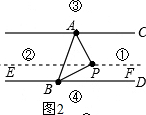
∴∠PAC=∠APQ,
∵∠APB=∠PAC+∠PBD,
又∵∠APB=∠APQ+∠BPQ,
∴∠BPQ=∠PBD,
∴PQ∥BD,
∴AC∥BD;
(2)∠APB=360°-(∠PAC+∠PBD);
(3)如图:以AB所在直线为分界,
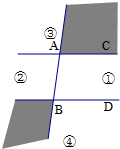
区域③的右侧和区域④的左侧(包括直线AB所属区域③④部分).
(1)AC∥BD,
理由如下:过点P作PQ∥AC,如图2,

∴∠PAC=∠APQ,
∵∠APB=∠PAC+∠PBD,
又∵∠APB=∠APQ+∠BPQ,
∴∠BPQ=∠PBD,
∴PQ∥BD,
∴AC∥BD;
(2)∠APB=360°-(∠PAC+∠PBD);
(3)如图:以AB所在直线为分界,

区域③的右侧和区域④的左侧(包括直线AB所属区域③④部分).
点评:本题主要考查平行线的判定和性质,掌握平行线的判定和性质是解题的关键,即①两直线平行?同位角相等,②两直线平行?内错角相等,③两直线平行?同旁内角互补,④a∥b,b∥c?a∥c.

练习册系列答案
相关题目
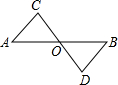 如图,AB与CD相交于点O,且△AOC≌△BOD,有下列结论:
如图,AB与CD相交于点O,且△AOC≌△BOD,有下列结论:(1)AO=BO,(2)AC=BD,(3)O是CD的中点,(4)∠A=∠D,(5)AC∥BD,
其中结论正确的个数是( )
| A、2 | B、3 | C、4 | D、5 |
下列各式变形正确的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列计算正确的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
| ||||
E、
|
 如图所示,已知∠AOB,OC平分∠AOB,
如图所示,已知∠AOB,OC平分∠AOB,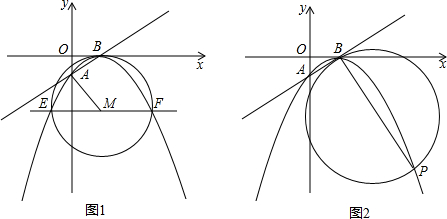
 如图△ABC中,CD⊥AB于点D,EF⊥AB于点F,∠1+∠B=180°,∠4与∠2相等吗?请阅读以下说明过程,并补全所空内容.
如图△ABC中,CD⊥AB于点D,EF⊥AB于点F,∠1+∠B=180°,∠4与∠2相等吗?请阅读以下说明过程,并补全所空内容. 如图,已知a∥b,a不垂直于c,BA,DA,DC,BC分别是同旁内角角平分线,则与∠ABC相等的角有( )个.
如图,已知a∥b,a不垂直于c,BA,DA,DC,BC分别是同旁内角角平分线,则与∠ABC相等的角有( )个.