题目内容
8.已知直线y=$\frac{4}{3}$x-4与x轴和y轴的交点分别为A、B.(1)求△ABO的面积;
(2)求△ABO的边AB上的高;
(3)求x轴上的一点C,使∠ABC=90°.
分析 (1)先求得A、B的坐标,从而求得OA=3,OB=4,然后根据三角形面积公式求得即可;
(2)作OD⊥AB于D,根据勾股定理求得AB=5,然后根据三角形面积公式得到$\frac{1}{2}$AB•OD=6,从而求得OD的值;
(3)根据蛇油=射影定理得到OB2=OC•OA,从而求得OC的长,即可求得C的坐标.
解答 解:(1)∵直线y=$\frac{4}{3}$x-4与x轴和y轴的交点分别为A、B.
∴令y=0,求得x=3,令x=0,求得y=-4,
∴A(3,0),B(0,-4),
∴△ABO的面积:$\frac{1}{2}$×3×4=6;
(2)∵OA=3,OB=4,
∴根据勾股定理求得AB=5,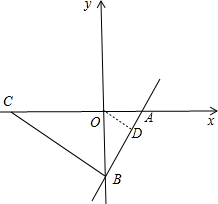
如图,作OD⊥AB于D,
∵$\frac{1}{2}$AB•OD=6,
∴OD=$\frac{12}{5}$,
∴△ABO的边AB上的高为$\frac{12}{5}$;
(3)如图,∵∠ABC=90°,
∴OB2=OC•OA,
∴OC=$\frac{O{B}^{2}}{OA}$=$\frac{{4}^{2}}{3}$=$\frac{16}{3}$,
∴C(-$\frac{16}{3}$,0).
点评 此题考查了一次函数图象上点的坐标特征以及三角形面积的综合运用,本题要求学生掌握一次函数与坐标轴交点的求法,与x轴交点的横坐标为令y=0求出的x的值;与y轴交点的纵坐标为令x=0求出的y的值,确定出与坐标轴的交点坐标.一次函数的图象与两坐标轴常围成直角三角形,解决这类问题一般需要利用点的坐标表示出线段的长度,从而根据三角形的面积公式来求解.

练习册系列答案
相关题目
18.已知P1(-2,y1),P2(3,y2)是一次函数y=-x+b(b为常数)的图象上的两个点,则y1,y2的大小关系是( )
| A. | y1<y2 | B. | y1>y2 | C. | y1=y2 | D. | 不能确定 |
 如图,以40m/s的速度将小球沿与地面成某一角度的方向击出时,小球的飞行路线将是一条抛物线.如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间(单位:s)之间具有函数关系h=20t-5t2.请解答以下问题:
如图,以40m/s的速度将小球沿与地面成某一角度的方向击出时,小球的飞行路线将是一条抛物线.如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间(单位:s)之间具有函数关系h=20t-5t2.请解答以下问题: 已知△ABC中.D、E、F各是三分之一点,确定S△DEF:S△ABC.
已知△ABC中.D、E、F各是三分之一点,确定S△DEF:S△ABC. 已知:如图,BE平分∠ABC,CE平分∠ACD,且交BE于点E.试说明:点E到∠FAC两边的距离相等.
已知:如图,BE平分∠ABC,CE平分∠ACD,且交BE于点E.试说明:点E到∠FAC两边的距离相等.