题目内容
16．
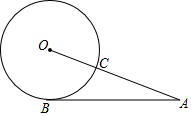如图，线段AB与⊙O相切于点B，线段AO与⊙O相交于点C，AB=12，AC=8，则⊙O的半径长为5．
分析 连接OB，根据切线的性质求出∠ABO=90°，在△ABO中，由勾股定理即可求出⊙O的半径长．
解答 
解：连接OB，
∵AB切⊙O于B，
∴OB⊥AB，
∴∠ABO=90°，
设⊙O的半径长为r，
由勾股定理得：
r2+122=（8+r）2，
解得r=5．
故答案为：5．
点评 本题考查了切线的性质和勾股定理的应用，关键是得出直角三角形ABO，主要培养了学生运用性质进行推理的能力．
练习册系列答案
相关题目
7．将二次函数y=x2的图象先向下平移1个单位，再向右平移3个单位，得到的图象与一次函数y=2x+b的图象有公共点，则实数b的取值范围是（ ）
| A． | b＞8 | B． | b＞-8 | C． | b≥8 | D． | b≥-8 |
如图，菱形ABCD中，∠A=60°，BD=6，则菱形ABCD的周长为24．
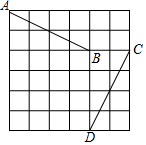如图，A点的坐标为（-1，5），B点的坐标为（3，3），C点的坐标为（5，3），D点的坐标为（3，-1），小明发现：线段AB与线段CD存在一种特殊关系，即其中一条线段绕着某点旋转一个角度可以得到另一条线段，你认为这个旋转中心的坐标是（1，1）或（4，4）．
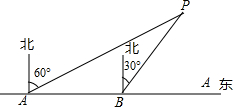为了维护国家主权和海洋权利，海监部门对我国领海实现了常态化巡航管理，如图，正在执行巡航任务的海监船以每小时50海里的速度向正东方航行，在A处测得灯塔P在北偏东60°方向上，继续航行1小时到达B处，此时测得灯塔P在北偏东30°方向上．