题目内容
15.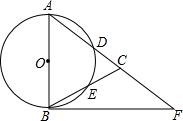 如图,△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在A的延长线上,且∠A=2∠CBF.
如图,△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在A的延长线上,且∠A=2∠CBF.(1)求证:BF是⊙O的切线;
(2)若AB=5,sin∠CBF=$\frac{\sqrt{5}}{5}$,求BC和BF的长.
分析 (1)连接AE,根据圆周角的性质求得AE⊥BC,根据等腰三角形的性质三效合一的性质得出∠BAE=∠CAE=$\frac{1}{2}$BAC,进而根据已知条件即可证明∠ABF=90°,从而证明BF是⊙O的切线;
(2)点C作CG∥BF,在Rt△ABE中可求得BE,进一步求得BC,在Rt△CGB中求出CG和GB,再利用平行线分线段成比例可求得.
解答 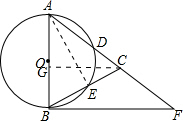 (1)证明:连接AE,
(1)证明:连接AE,
∵AB为直径,
∴AE⊥BC,
∵AB=AC,
∴∠BAE=∠CAE=$\frac{1}{2}$BAC,
∴∠A=2∠CBF,
∴∠CBF=∠BAE,
∵∠BAE+∠ABE=90°,
∴∠ABF=∠ABE+∠CBF=90°,
∵AB为⊙O直径,
∴BF是⊙O的切线;
(2)解:过点C作CG⊥AB于点G,
∵sin∠CBF=$\frac{\sqrt{5}}{5}$,∠BAE=∠CBF,
∴sin∠BAE=sin∠CBF=$\frac{\sqrt{5}}{5}$,
∵∠AEB=90°,AB=5,
∴BE=AB•sin∠∠BAE=$\sqrt{5}$,
∵AB=AC,∠AEB=90°,
∴BC=2BE=2$\sqrt{5}$,
在Rt△ABE中,由勾股定理得AE=$\sqrt{A{B}^{2}-B{E}^{2}}$=$\sqrt{{5}^{2}-(\sqrt{5})^{2}}$=2$\sqrt{5}$,
∴sin∠ABE=$\frac{AE}{AB}$=$\frac{2\sqrt{5}}{5}$,cos∠ABE=$\frac{BE}{AB}$=$\frac{\sqrt{5}}{5}$,
在Rt△CBG中,sin∠ABE=$\frac{CG}{BC}$=$\frac{2\sqrt{5}}{5}$,cos∠ABE=$\frac{BG}{BC}$=$\frac{\sqrt{5}}{5}$,
∴GC=4,GB=2,
∴AG=3,
∵GC∥BF,
∴△AGC∽△ABF,
∴$\frac{GC}{BF}$=$\frac{AG}{AB}$,
∴BF=$\frac{GC•AB}{AG}$=$\frac{4×5}{3}$=$\frac{20}{3}$.
点评 本题考查了圆的切线的判定定理、圆周角定理、等腰三角形的性质及平行线分线段定理的应用,解题的关键是如何利用已知条件中的sin∠CBF=$\frac{\sqrt{5}}{5}$,属于中档题,有一定的难度.

 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案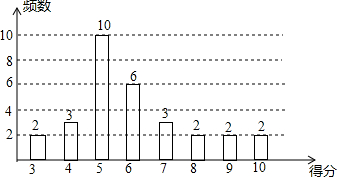 为了普及环保知识,增强环保意识,某中学随机抽取了30名学生参加环保知识测试,得分(10分制)如图所示,假设得分值的中位数为m,众数为n,平均数为$\overline x$,则( )
为了普及环保知识,增强环保意识,某中学随机抽取了30名学生参加环保知识测试,得分(10分制)如图所示,假设得分值的中位数为m,众数为n,平均数为$\overline x$,则( )| A. | m=n=$\overline x$ | B. | m=n<$\overline x$ | C. | m<n<$\overline x$ | D. | n<m<$\overline x$ |
| A. | 540° | B. | 720° | C. | 960° | D. | 1080° |
 ⊙O是△ABC的外接圆,且AB=AC,点D在$\widehat{AB}$上运动(不与B,C点重合),过点D作DE∥BC,与AB的延长线交于点E,连接AD、BD.
⊙O是△ABC的外接圆,且AB=AC,点D在$\widehat{AB}$上运动(不与B,C点重合),过点D作DE∥BC,与AB的延长线交于点E,连接AD、BD.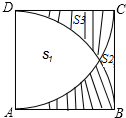 如图,已知正方形ABCD,AB=1,弧BD与弧AC都是以1为半径的圆弧,求S1-S2的值是多少?(提示:设S1、S2、S3分别为x、y、z,列方程组求解)
如图,已知正方形ABCD,AB=1,弧BD与弧AC都是以1为半径的圆弧,求S1-S2的值是多少?(提示:设S1、S2、S3分别为x、y、z,列方程组求解)