题目内容
5.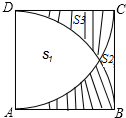 如图,已知正方形ABCD,AB=1,弧BD与弧AC都是以1为半径的圆弧,求S1-S2的值是多少?(提示:设S1、S2、S3分别为x、y、z,列方程组求解)
如图,已知正方形ABCD,AB=1,弧BD与弧AC都是以1为半径的圆弧,求S1-S2的值是多少?(提示:设S1、S2、S3分别为x、y、z,列方程组求解)
分析 图中S1、S2、S3、S4图形的面积和为正方形的面积,S1+S3=S1+S4=扇形的面积,因此两个扇形的面积的和-正方形的面积=S1-S2,即 $\frac{90π×1×2}{360}$-1=$\frac{π}{2}$-1.
解答  解:如图:正方形的面积=S1+S2+S3+S4;①
解:如图:正方形的面积=S1+S2+S3+S4;①
两个扇形的面积=2S1+S3+S4;②
②-①,得:S1-S2=S扇形-S正方形=$\frac{90π×1×2}{360}$-1=$\frac{π}{2}$-1.
答:S1-S2的值是$\frac{π}{2}$-1.
点评 本题主要考查了扇形的面积计算公式及不规则图形的面积计算方法.找出正方形内四个图形面积之间的联系是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.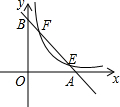 如图,已知直线y=-x+3分别与x轴,y轴交于A,B两点,与双曲线y=$\frac{k}{x}$交于E,F两点.若AB=3EF,则k的值是( )
如图,已知直线y=-x+3分别与x轴,y轴交于A,B两点,与双曲线y=$\frac{k}{x}$交于E,F两点.若AB=3EF,则k的值是( )
 如图,已知直线y=-x+3分别与x轴,y轴交于A,B两点,与双曲线y=$\frac{k}{x}$交于E,F两点.若AB=3EF,则k的值是( )
如图,已知直线y=-x+3分别与x轴,y轴交于A,B两点,与双曲线y=$\frac{k}{x}$交于E,F两点.若AB=3EF,则k的值是( )| A. | $\frac{\sqrt{6}}{2}$ | B. | 2 | C. | $\frac{5}{4}$ | D. | $\frac{3}{4}$ |
13.关于x的两个多项式乘积:(x+a)(x+b)的结果是( )
| A. | x2-ab | B. | x2+ab | C. | x2+(a-b)x+ab | D. | x2+(a+b)x+ab |
10.下列命题中的假命题是( )
| A. | 当a=b时,有a2=b2 | |
| B. | 经过已知直线外一点,有且只有一条直线与已知直线平行 | |
| C. | 互为相反数的两个数的和为0 | |
| D. | 相等的角是对顶角 |
15.如果a=(-2009)0,b=(-0.1)-1,c=(-$\frac{3}{2}$)2,那么a、b、c三个数的大小为( )
| A. | a>b>c | B. | c>a>b | C. | a>c>b | D. | c>b>a |
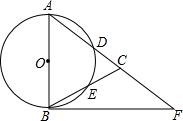 如图,△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在A的延长线上,且∠A=2∠CBF.
如图,△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在A的延长线上,且∠A=2∠CBF. 如图,直线AB和CD相交于点O,FO⊥CD于点O,∠1=∠3,试判断EO与AB有何特殊位置关系,并说明理由.
如图,直线AB和CD相交于点O,FO⊥CD于点O,∠1=∠3,试判断EO与AB有何特殊位置关系,并说明理由.