题目内容
2.将一条长为40cm的铁丝剪成两段,并以每一段铁丝的长度为周长各做成一个正方形,则这两个正方形面积之和的最小值是50cm2.分析 根据正方形面积和周长的转化关系“正方形的面积=$\frac{1}{16}$×周长×周长”列出面积的函数关系式并求得最小值.
解答 解:设一段铁丝的长度为x,另一段为(40-x),则边长分别为x,$\frac{1}{4}$(40-x),
则S=$\frac{1}{16}$x2+$\frac{1}{16}$(40-x)(40-x)=$\frac{1}{16}$(x-20)2+50,
∴由函数当x=20cm时,S最小,为50cm2.
故答案为:50.
点评 本题考查了二次函数的最值的知识,解题的关键是能够从实际问题中整理出二次函数模型,难度不大.

练习册系列答案
相关题目
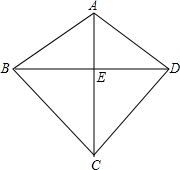 如图,平面上的四边形ABCD是一只“风筝”的骨架,其中AB=AD,CB=CD,某同学观察了这只“风筝”的骨架后,认为四边形ABCD的两条对角线AC,BD垂直,垂足为E,并且BE=ED,你同意这位同学的判断吗?请说明理由.
如图,平面上的四边形ABCD是一只“风筝”的骨架,其中AB=AD,CB=CD,某同学观察了这只“风筝”的骨架后,认为四边形ABCD的两条对角线AC,BD垂直,垂足为E,并且BE=ED,你同意这位同学的判断吗?请说明理由.