题目内容
14．若二次函数y=（m+1）x2+m2-9的图象经过原点且有最大值，则m=-3．分析 此题可以将原点坐标（0，0）代入y=（m+1）x2+m2-9，求得m的值，然后根据有最大值确定m的值即可．
解答 解：由于二次函数y=（m+1）x2+m2-9的图象经过原点，
代入（0，0）得：m2-9=0，
解得：m=3或m=-3；
又∵有最大值，
∴m+1＜0，
∴m=-3．
故答案为：-3；
点评 本题考查了二次函数图象上点的坐标特征，通过代入点的坐标即可求解，较为简单．
练习册系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
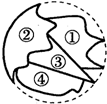一圆形玻璃被打碎后，其中四块碎片如图所示，若选择其中一块碎片带到商店，配制与原来大小一样的圆形玻璃，选择的是（ ）
9．与x轴无交点的抛物线是（ ）
| A． | y=2x2-3 | B． | y=x2+2x | C． | y=-$\frac{1}{3}$（x-1）2-1 | D． | y=-$\frac{1}{3}$x2+1 |
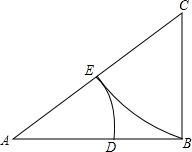已知小强将线段AB黄金分割（点D为黄金分割点）所作的图形如图所示．请你回答：