题目内容
4.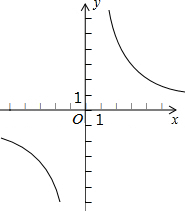 反比例函数y=$\frac{k}{x}$(k≠0)过A(3,4),点B与点A关于直线y=2对称,抛物线y=-x2+bx+c过点B和C(0,3).
反比例函数y=$\frac{k}{x}$(k≠0)过A(3,4),点B与点A关于直线y=2对称,抛物线y=-x2+bx+c过点B和C(0,3).(1)求反比例函数的表达式;
(2)求抛物线的表达式;
(3)若抛物线y=-x2+bx+m在-2≤x<2的部分与y=$\frac{k}{x}$无公共点,求m的取值范围.
分析 (1)将点(3,4)代入反比例函数的解析式即可求出k的值.
(2)求出点B的坐标,然后将B与C的坐标代入即可求出抛物线的解析式即可求出b与c的值.
(3)令x=2和-2代入反比例函数中求出相应的点坐标,然后将两点的坐标代入y=-x2+2x+m中求出m的值
解答 解:(1)∵反比例函数y=$\frac{k}{x}$过A(3,4),
∴k=12,
∴y=$\frac{12}{x}$
(2)∵点B与点A关于直线y=2对称,
∴B(3,0).
∵抛物线y=-x2+bx+c过点B和C(0,3)
∴$\left\{\begin{array}{l}{-9+3b+c=0}\\{c=3}\end{array}\right.$
∴$\left\{\begin{array}{l}{b=2}\\{c=3}\end{array}\right.$
∴y=-x2+2x+3
(3)反比例函数的解析式:y=$\frac{12}{x}$
令x=-2时,y=-6,即(-2,-6)
令x=2时,y=6,即(2,6)
当y=-x2+2x+m过点(-2,-6)时,m=2
当当y=-x2+2x+m过点(2,6)时,m=6
∴y=-x2+2x+m在-2≤x<2的部分与y=$\frac{12}{x}$无公共点时,此时m的范围:2<m≤6,
点评 本题考查二次函数的综合问题,解题的关键是求出相关点的坐标,然后利用待定系数法求出系数的值,本题属于中等题型.

练习册系列答案
相关题目
19.将二次函数y=x2的图象向下平移2个单位,再向右平移3个单位,则平移后的二次函数的解析式为( )
| A. | y=x2-2 | B. | y=x2+2 | C. | y=(x+3)2+2 | D. | y=(x-3)2-2 |
20.实数$\sqrt{2}$的相反数是( )
| A. | -$\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | -$\sqrt{2}$ | D. | $\sqrt{2}$ |
17.若关于x的不等式3-x>a的解集为x<4,则关于m的不等式2m+3a<1的解为( )
| A. | m<2 | B. | m>1 | C. | m>-2 | D. | m<-1 |
4.下列四个关系式:①y=|x|;②|y|=x;③2x2-y=0;④2x-y2=0,其中y是x的函数的是( )
| A. | ①②③④ | B. | ①②③ | C. | ①③ | D. | ②④ |
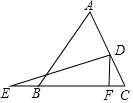 如图,在△ABC中,D在AC边上,DF⊥BC于F,∠E+∠A=∠C,AB=DE.若CF=$\sqrt{5}$,则BE=2$\sqrt{5}$.
如图,在△ABC中,D在AC边上,DF⊥BC于F,∠E+∠A=∠C,AB=DE.若CF=$\sqrt{5}$,则BE=2$\sqrt{5}$.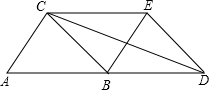 如图,平移△ABC到△BDE的位置,且点D在边AB的延长线上,连接EC,CD,若AB=BC,那么在以下四个结论:①四边形ABEC是平行四边形;②四边形BDEC是菱形;③AC⊥DC;④DC平分∠BDE,正确的有①②③④.
如图,平移△ABC到△BDE的位置,且点D在边AB的延长线上,连接EC,CD,若AB=BC,那么在以下四个结论:①四边形ABEC是平行四边形;②四边形BDEC是菱形;③AC⊥DC;④DC平分∠BDE,正确的有①②③④.