题目内容
7.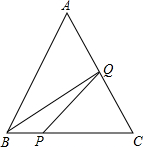 在△ABC中,已知AB=BC=CA=4cm,点P、Q分别从B、C两点同时出发,其中点P沿BC向终点C运动,速度为1cm/s;点Q沿CA、AB向终点B运动,速度为2cm/s,设它们运动的时间为x(s),当x=2或$\frac{16}{5}$,△BPQ是直角三角形.
在△ABC中,已知AB=BC=CA=4cm,点P、Q分别从B、C两点同时出发,其中点P沿BC向终点C运动,速度为1cm/s;点Q沿CA、AB向终点B运动,速度为2cm/s,设它们运动的时间为x(s),当x=2或$\frac{16}{5}$,△BPQ是直角三角形.
分析 用t表示出BP、CQ、BQ,然后分两种情况:①∠BPQ=90°,②∠BQP=90°进行讨论即可得解.
解答 解:根据题意,得BP=tcm,CQ=2tcm,BQ=(8-2t)cm,
若△BPQ是直角三角形,则∠BPQ=90°或∠BQP=90°,
①当∠BPQ=90°时,
Q在A点,CQ=CA=4cm,
4÷2=2(s);
②当∠BQP=90°时,∵∠B=60°,
∴∠BPQ=90°-60°=30°,
∴BQ=$\frac{1}{2}$BP,
即8-2t=$\frac{1}{2}$t,
解得t=$\frac{16}{5}$,
故当t=2或$\frac{16}{5}$秒时,△BPQ是直角三角形.
故答案为:2或$\frac{16}{5}$.
点评 本题考查了等边三角形的性质,一元二次方程的应用,解题的关键是根据实际问题分两种情况讨论.

练习册系列答案
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
15.小聪在画一次函数时,当他列表后,发现题中一次函数y=◆x+◆中的k和b看不清了,则( )
| x | 0 | 3 |
| y | 2 | 0 |
| A. | k=2,b=3 | B. | k=-$\frac{2}{3}$,b=2 | C. | k=3,b=2 | D. | k=1,b=-1 |
12.计算-2×(210)的结果等于( )
| A. | -211 | B. | -410 | C. | 211 | D. | 411 |
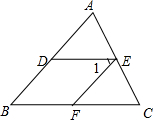 如图,∠AED=∠C,∠1=∠B,请说明:EF∥AB.
如图,∠AED=∠C,∠1=∠B,请说明:EF∥AB. 已知:如图在△ABC,△ADE中,∠BAC=∠DAE+90°,AB=AC,AD=AE.点C,D,E三点在同一条直线上,连接BD,BE.以下两个结论:
已知:如图在△ABC,△ADE中,∠BAC=∠DAE+90°,AB=AC,AD=AE.点C,D,E三点在同一条直线上,连接BD,BE.以下两个结论: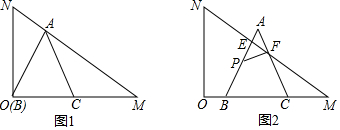
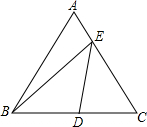 如图,在边长为4的等边△ABC中,D为BC的中点,E是AC边上一点,则BE+DE的最小值为2$\sqrt{7}$.
如图,在边长为4的等边△ABC中,D为BC的中点,E是AC边上一点,则BE+DE的最小值为2$\sqrt{7}$.