题目内容
15.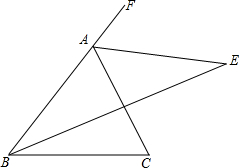 如图,在△ABC中,∠B的平分线与∠BAC的外角平分线相交于点E.
如图,在△ABC中,∠B的平分线与∠BAC的外角平分线相交于点E.(1)若∠C=78°,求∠E的度数;
(2)若∠C=α,请直接写出∠E的度数.(用含α的代数式表示)
分析 (1)根据角平分线的性质得到∠1=$\frac{1}{2}$∠FAC,∠2=$\frac{1}{2}∠$ABC,根据外角的性质得到∠1=∠2+∠E,∠FAC=∠ABC+∠C,根据等量代换即可得到结论;
(2)由(1)证得:∠E=$\frac{1}{2}$∠C,结论可得.
解答 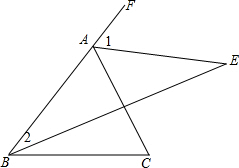 解:(1)∵AE平分∠CAF,
解:(1)∵AE平分∠CAF,
∴∠1=$\frac{1}{2}$∠FAC,∠1=∠2+∠E,
∵BE平分∠ABC,
∴∠2=$\frac{1}{2}∠$ABC,
∵∠1=∠2+∠E,∠FAC=∠ABC+∠C,
∴$\frac{1}{2}$∠FAC=$\frac{1}{2}$∠ABC+∠E,
∴$\frac{1}{2}$(∠ABC+∠C)=$\frac{1}{2}$∠ABC+∠E,
∴∠E=$\frac{1}{2}$∠C=$\frac{1}{2}×$78°,
(2)由(1)证得:∠E=$\frac{1}{2}$∠C,
∵∠C=α,
∴∠E=$\frac{1}{2}α$.
点评 本题考查的三角形的外角的性质,关键是掌握三角形的外角等于不相邻两个内角的和,利用∠ACE是△ABC的外角和∠DCE是△BCD的外角的性质便可求得∠A=2∠D.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
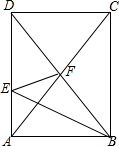 如图,矩形ABCD的面积为36,BE平分∠ABD,交AD于E,沿BE将△ABE折叠,点A的对应点刚好落在矩形两条对角线的交点F处,则△ABE的面积为6.
如图,矩形ABCD的面积为36,BE平分∠ABD,交AD于E,沿BE将△ABE折叠,点A的对应点刚好落在矩形两条对角线的交点F处,则△ABE的面积为6. 已知,如图,在四边形ABCD中,AC=BD,且相交于点O,E,F为AB,CD的中点,EF分别交AC,BD于点G,H,求证:OG=OH.
已知,如图,在四边形ABCD中,AC=BD,且相交于点O,E,F为AB,CD的中点,EF分别交AC,BD于点G,H,求证:OG=OH. 如图,正方形ABCD中,E为CD的中点,F是DA的中点,连接BE,与CF相交于P,求证:AP=AB.
如图,正方形ABCD中,E为CD的中点,F是DA的中点,连接BE,与CF相交于P,求证:AP=AB. 如图,已知AB∥CD,BE平分∠ABF,DF平分∠CDE,若∠E=70°,∠F=65°,则∠BGD=90°.
如图,已知AB∥CD,BE平分∠ABF,DF平分∠CDE,若∠E=70°,∠F=65°,则∠BGD=90°.