题目内容
设I是△ABC的内心，BC=AC+AI，∠ABC-∠ACB=12°，则∠BAC= ．
考点：三角形的内切圆与内心
专题：
分析：如图，作辅助线；证明BG=AI，此为解决该题的核心结论；证明∠BAC=2∠ABC，结合已知条件、三角形的内角和定理即可解决问题．
解答：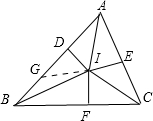
解：如图，在BD上截取DG=AD，连接GI；
设点D、E、F分别为△ABC内切圆的切点，
则AD=AE（设为λ），BD=BF（设为μ），CE=CF（设为η）；
DI⊥AG；而AD=DG，
∴DI为AG的垂直平分线，
∴GI=AI；
∵BC=AC+AI，即μ+η=λ+η+AI，
∴μ-λ=AI，即BG=AI，
∴BG=GI=AI，
∴∠GBI=∠GIB（设为α），∠AGI=∠GAI（设为β）；
∵∠AGI=∠GBI+∠GIB=2α，
∴∠GAI=∠AGI=β=2α；
∵∠BAC=2β，∠ABC=2α，
∴∠BAC=2∠ABC，而∠ABC-∠ACB=12°，
∠BAC+∠ABC+∠ACB=180°，
∴∠BAC=96°，
故答案为96°．
解：如图，在BD上截取DG=AD，连接GI；设点D、E、F分别为△ABC内切圆的切点，
则AD=AE（设为λ），BD=BF（设为μ），CE=CF（设为η）；
DI⊥AG；而AD=DG，
∴DI为AG的垂直平分线，
∴GI=AI；
∵BC=AC+AI，即μ+η=λ+η+AI，
∴μ-λ=AI，即BG=AI，
∴BG=GI=AI，
∴∠GBI=∠GIB（设为α），∠AGI=∠GAI（设为β）；
∵∠AGI=∠GBI+∠GIB=2α，
∴∠GAI=∠AGI=β=2α；
∵∠BAC=2β，∠ABC=2α，
∴∠BAC=2∠ABC，而∠ABC-∠ACB=12°，
∠BAC+∠ABC+∠ACB=180°，
∴∠BAC=96°，
故答案为96°．
点评：该题主要考查了三角形内切圆的性质及其应用问题；解题的关键是作辅助线，灵活运用内切圆的性质、切线长定理等几何知识点来分析、判断．
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
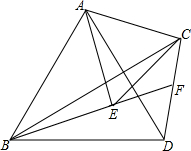如图，在△ABC中，分别以AB、AC为边作等边△ABD与等边△ACE，连接BE、CD，BE的延长线与CD交于点F，连接AF，有以下四个结论：
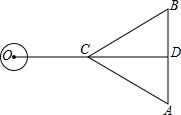如图，CD为等边三角形ABC的高，点O在DC的延长线上，且OD=11，CD=6，⊙O的半径为1，若将⊙O绕点C按顺时针方向旋转360°，在旋转过程中，⊙O与等边三角形ABC的边只有一个公共点的情况一共出现（ ）
在△ABC中，∠A=60°，以BC为直径作圆O交AC于点D，交AB于点E，连接DE，BD，CE．试证明：△ADE∽△ABC．
圆锥形的烟囱帽的底面直径是80cm，母线长为50cm．