题目内容
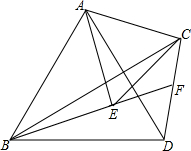如图，在△ABC中，分别以AB、AC为边作等边△ABD与等边△ACE，连接BE、CD，BE的延长线与CD交于点F，连接AF，有以下四个结论：①BE=CD；②FA平分∠EFC；③FE=FD；④FE+FC=FA．
其中正确的结论有
考点：全等三角形的判定与性质,等边三角形的性质
专题：
分析：连接AF，在AF上找到点G使得FG=EF，易证△BAE≌△DAC，可得BE=CD，①正确；易证A、E、F、C四点共圆，根据AE=AC，可得FA平分∠EFC，②正确；易证△AGE≌△CFE，可得AG=CF，即可求得AF=CF+EF，④正确；
解答：解：连接AF，在AF上找到点G使得FG=EF，
∵∠BAE+∠DAE=60°，∠CAD+∠DAE=60°，
∴∠BAE=∠DAC，
在△BAE和△DAC中，
，
∴△BAE≌△DAC，（SAS）
∴BE=CD，①正确；
∠BEA=∠ACD，
∵∠AEB+∠AEF=180°，
∴∠AEF+∠ACF=180°，
∴A、E、F、C四点共圆，
∴∠EFC=120°，
∵AE=AC，
∴∠AFC=∠AFE，即FA平分∠EFC，②正确；
∵FG=EF，∠AFE=60°，
∴△EFG是等边三角形，
∴EF=EG，
∵∠AEG+∠CEG=60°，∠CEG+∠CEF=60°，
∴∠AEG=∠CEF，
在△AGE和△CFE中，
，
∴△AGE≌△CFE（SAS），
∴AG=CF，
∵AF=AG+FG，
∴AF=CF+EF，④正确；
∵CF+EF=AF，CF+DF=CD，
CD≠AF，
∴FE=FD，③错误，
故答案为 ①②④．
∵∠BAE+∠DAE=60°，∠CAD+∠DAE=60°，
∴∠BAE=∠DAC，
在△BAE和△DAC中，
|
∴△BAE≌△DAC，（SAS）
∴BE=CD，①正确；
∠BEA=∠ACD，
∵∠AEB+∠AEF=180°，
∴∠AEF+∠ACF=180°，
∴A、E、F、C四点共圆，
∴∠EFC=120°，
∵AE=AC，
∴∠AFC=∠AFE，即FA平分∠EFC，②正确；
∵FG=EF，∠AFE=60°，
∴△EFG是等边三角形，
∴EF=EG，
∵∠AEG+∠CEG=60°，∠CEG+∠CEF=60°，
∴∠AEG=∠CEF，
在△AGE和△CFE中，
|
∴△AGE≌△CFE（SAS），
∴AG=CF，
∵AF=AG+FG，
∴AF=CF+EF，④正确；
∵CF+EF=AF，CF+DF=CD，
CD≠AF，
∴FE=FD，③错误，
故答案为 ①②④．
点评：本题考查了全等三角形的判定，考查了全等三角形对应边相等的性质，考查了圆周角原理，本题中求证△BAE≌△DAC和△AGE≌△CFE是解题的关键．
练习册系列答案
相关题目
已知关于x的方程2x2-3kx+k=0的一个根为1，则它的另一个根及k的值分别为（ ）
A、
| ||
B、1，
| ||
C、2，
| ||
D、
|
如图，顺次连接正方形ABCD的四边中点得到正方形①，再顺次连接正方形①的四边得到正方形②，依此规律继续连接可得到正方形③，正方形④，…观察如图所示前三个图形及数的规律，则第四个□的数是 （ ）
A、
| ||||
| B、3 | ||||
C、
| ||||
D、
|
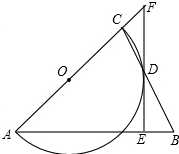如图，△ABC是等腰三角形，AB=AC，以AC为直径的⊙O与BC交于点D，DE⊥AB，垂足为E，ED的延长线与AC的延长线交于点F．