题目内容
6.已知$\sqrt{x}$($\sqrt{x}$+$\sqrt{y}$)=3$\sqrt{y}$($\sqrt{x}$+5$\sqrt{y}$),求$\frac{2x+\sqrt{xy}+3y}{x+\sqrt{xy}-y}$的值.分析 首先对已知的式子进行变形,利用x和y表示出$\sqrt{xy}$,则可以把所求的式子进行化简,然后进一步化简利用y表示出x,代入即可求解.
解答 解:∵$\sqrt{x}$($\sqrt{x}$+$\sqrt{y}$)=3$\sqrt{y}$($\sqrt{x}$+5$\sqrt{y}$),
∴x+$\sqrt{xy}$=3$\sqrt{xy}$+15y,
∴$\sqrt{xy}$=$\frac{1}{2}$(x-15y),
则原式=$\frac{2x+\frac{1}{2}(x-15y)+3y}{x+\frac{1}{2}(x-15y)-y}$=$\frac{4x+x-15y+6y}{2x+x-15y-2y}$=$\frac{5x-9y}{3x-17y}$.
x+$\sqrt{xy}$=3$\sqrt{xy}$+15y,
即x-2$\sqrt{xy}$-15y=0,
($\sqrt{x}$-5$\sqrt{y}$)($\sqrt{x}$+3$\sqrt{y}$)=0,
∴$\sqrt{x}$-5$\sqrt{y}$=0,则x=25y.
则原式=$\frac{125y-9y}{75y-17y}$=$\frac{116y}{58y}$=$\frac{58}{29}$.
点评 本题考查了二次根式的化简求值,正确对已知的式子进行变形,利用y表示出x是关键.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
14.若一次函数y=kx+b的图象经过一、三、四象限,则y=bx+k的图象经过( )象限.
| A. | 一、三、四 | B. | 二、三、四 | C. | 一、二、四 | D. | 一、二、三 |
11.下列说法正确的是( )
| A. | 每个命题都有逆命题 | B. | 每个定理都有逆定理 | ||
| C. | 所有命题都是定理 | D. | 假命题的逆命题都是假命题 |
18.若一元二次方程ax2+bx+c=0的一个根为-1,则( )
| A. | a+b+c=0 | B. | a-b+c=0 | C. | -a-b+c=0 | D. | -a+b+c=0 |
16. 如图所示,一场暴雨过后,垂直于地面的一棵树在距地面1米处折断,树尖B恰好碰到地面,此时一只蚂蚁正好位于折断处并朝着树尖的方向爬行,爬行速度是每分钟0.5米,经测量AB长2米,则蚂蚁爬到B处需要多久( )
如图所示,一场暴雨过后,垂直于地面的一棵树在距地面1米处折断,树尖B恰好碰到地面,此时一只蚂蚁正好位于折断处并朝着树尖的方向爬行,爬行速度是每分钟0.5米,经测量AB长2米,则蚂蚁爬到B处需要多久( )
 如图所示,一场暴雨过后,垂直于地面的一棵树在距地面1米处折断,树尖B恰好碰到地面,此时一只蚂蚁正好位于折断处并朝着树尖的方向爬行,爬行速度是每分钟0.5米,经测量AB长2米,则蚂蚁爬到B处需要多久( )
如图所示,一场暴雨过后,垂直于地面的一棵树在距地面1米处折断,树尖B恰好碰到地面,此时一只蚂蚁正好位于折断处并朝着树尖的方向爬行,爬行速度是每分钟0.5米,经测量AB长2米,则蚂蚁爬到B处需要多久( )| A. | $\frac{{\sqrt{5}}}{2}$分钟 | B. | $\sqrt{3}$分钟 | C. | ($\sqrt{5}$+1)分钟 | D. | $2\sqrt{5}$分钟 |
 △ABC中,∠BAC=70°,BC=12,AB的重直平分线交BC边于点E,交AB于点D,AC的垂直平分线交BC边于点N,交AC点于M.求:
△ABC中,∠BAC=70°,BC=12,AB的重直平分线交BC边于点E,交AB于点D,AC的垂直平分线交BC边于点N,交AC点于M.求: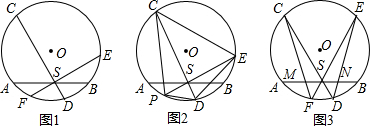
 已知:抛物线y=ax2+2x+c,对称轴为直线x=-1,抛物线与y轴交于点C,与x轴交于A(-3,0)、B两点.
已知:抛物线y=ax2+2x+c,对称轴为直线x=-1,抛物线与y轴交于点C,与x轴交于A(-3,0)、B两点.