题目内容
10. △ABC中,∠BAC=70°,BC=12,AB的重直平分线交BC边于点E,交AB于点D,AC的垂直平分线交BC边于点N,交AC点于M.求:
△ABC中,∠BAC=70°,BC=12,AB的重直平分线交BC边于点E,交AB于点D,AC的垂直平分线交BC边于点N,交AC点于M.求:(1)AN+AE;
(2)∠EAN的度数.
分析 (1)根据线段的垂直平分线得出BE=AE,AN=CN,从而可△AEN的周长=2BC;
(2)由BE=AE,AN=CN推出∠B=∠BAE,∠C=∠CAN,根据三角形的内角和定理求出∠B+∠C的度数,求出∠BAE+∠CAN的度数即可得到答案.
解答 解:(1)∵点E、N分别是AB、AC边的垂直平分线与BC的交点,
∴BE=AE,AN=CN.
∴△AEN的周长=AE+AN+EN=BE+NC+EN=2BC=24;
∴AN+AE=BC=12;
(2)∵BE=AE,AN=CN,
∴∠B=∠BAE,∠C=∠CAN.
∵∠BAC+∠B+∠C=180°,∠BAC=70°,
∴∠B+∠C=110°,
∴∠BAE+∠CAN=110°,
∴∠EAN=(∠BAE+∠CAN)-∠BAC=40°
点评 本题主要考查对三角形的内角和定理,线段的垂直平分线等知识点的理解和掌握,能综合运用这些性质进行计算是解此题的关键.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
18.下列比较有理数-0.1,-$\frac{1}{3}$,-$\frac{1}{4}$大小正确的是( )
| A. | -$\frac{1}{3}$<-$\frac{1}{4}$<-0.1 | B. | -$\frac{1}{4}$<-$\frac{1}{3}$<-0.1 | C. | -0.1<-$\frac{1}{4}$<-$\frac{1}{3}$ | D. | -0.1<-$\frac{1}{3}$<-$\frac{1}{4}$ |
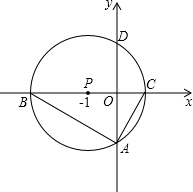 如图,以点P(-1,0)为圆心的圆,交x轴于B、C两点(B在C的左侧),交y轴于A、D两点(A在D的下方),AD=2,将△ABC绕点P旋转180°,得到△MCB.
如图,以点P(-1,0)为圆心的圆,交x轴于B、C两点(B在C的左侧),交y轴于A、D两点(A在D的下方),AD=2,将△ABC绕点P旋转180°,得到△MCB.