题目内容
16. 如图所示,一场暴雨过后,垂直于地面的一棵树在距地面1米处折断,树尖B恰好碰到地面,此时一只蚂蚁正好位于折断处并朝着树尖的方向爬行,爬行速度是每分钟0.5米,经测量AB长2米,则蚂蚁爬到B处需要多久( )
如图所示,一场暴雨过后,垂直于地面的一棵树在距地面1米处折断,树尖B恰好碰到地面,此时一只蚂蚁正好位于折断处并朝着树尖的方向爬行,爬行速度是每分钟0.5米,经测量AB长2米,则蚂蚁爬到B处需要多久( )| A. | $\frac{{\sqrt{5}}}{2}$分钟 | B. | $\sqrt{3}$分钟 | C. | ($\sqrt{5}$+1)分钟 | D. | $2\sqrt{5}$分钟 |
分析 直接利用勾股定理得出BC的长,再利用蚂蚁爬行速度得出答案.
解答 解:由题意可得:BC=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
∵蚂蚁爬行速度是每分钟0.5米,
∴蚂蚁爬到B处需要:$\frac{\sqrt{5}}{0.5}$=2$\sqrt{5}$(分钟).
故选:D.
点评 此题主要考查了勾股定理的应用,正确得出BC的长是解题关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
4.已知梯形的上、下底分别是1和5,则两腰可以是( )
| A. | 3和8 | B. | 4和8 | C. | 2和2 | D. | 3和5 |
11.计算7-4的结果是( )
| A. | 3 | B. | -3 | C. | 11 | D. | -11 |
1.若a-b+c=0,则关于x的一元二次方程ax2+bx+c=0必有一根为( )
| A. | 0 | B. | 1 | C. | -1 | D. | 2 |
8.下列命题中,真命题有( )
①点P(a,a)一定在第一象限角平分线上;
②点P(-a,-a)一定在第二象限的角平分线上;
③点P(x,y)关于x轴的对称点是(x,-y);
④点M(3,-2)到x轴的距离是3,到y轴的距离是2.
①点P(a,a)一定在第一象限角平分线上;
②点P(-a,-a)一定在第二象限的角平分线上;
③点P(x,y)关于x轴的对称点是(x,-y);
④点M(3,-2)到x轴的距离是3,到y轴的距离是2.
| A. | 0 个 | B. | 1个 | C. | 2个 | D. | 3个 |
6.下列四组线段中,可以构成直角三角形的是( )
| A. | 4,5,6 | B. | 1.5,2.5,3.5 | C. | 2,3,4 | D. | 9,12,15 |
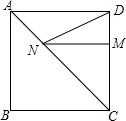 如图,正方形ABCD中,AB=7,M是DC上的一点,且DM=3,N是AC上的一动点,求|DN-MN|的最小值与最大值.
如图,正方形ABCD中,AB=7,M是DC上的一点,且DM=3,N是AC上的一动点,求|DN-MN|的最小值与最大值.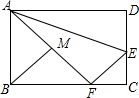 如图,在矩形ABCD中,AD=10,CD=6,E是CD边上一点,沿AE折叠△ADE,使点D恰好落在BC边上的F处,则$\frac{BF}{AF}$=$\frac{4}{5}$.
如图,在矩形ABCD中,AD=10,CD=6,E是CD边上一点,沿AE折叠△ADE,使点D恰好落在BC边上的F处,则$\frac{BF}{AF}$=$\frac{4}{5}$.