题目内容
3.等腰△ABC中,∠A=60°,其面积为$\frac{{7+4\sqrt{3}}}{27}$,它的内切圆面积为$\frac{7+4\sqrt{3}}{81\sqrt{3}}$π.分析 根据有一个角等于60°的三角形是等腰三角形,得到△ABC是等边三角形,设它的内切圆的半径为r,求出三角形的边长和高代入三角形的面积公式解得r2=$\frac{7+4\sqrt{3}}{81\sqrt{3}}$,于是得到内切圆面积为:$\frac{7+4\sqrt{3}}{81\sqrt{3}}$π,
解答 解:∵△ABC是等腰三角形.
∵∠A=60°,
∴△ABC是等边三角形,
设它的内切圆的半径为r,
∴BC=2$\sqrt{3}$r,高=3r,
∴S△ABC=$\frac{1}{2}$×2$\sqrt{3}$r•3r=$\frac{{7+4\sqrt{3}}}{27}$,
解得:r2=$\frac{7+4\sqrt{3}}{81\sqrt{3}}$,
∴内切圆面积为:$\frac{7+4\sqrt{3}}{81\sqrt{3}}$π.
故答案为:$\frac{7+4\sqrt{3}}{81\sqrt{3}}$π.
点评 本题考查了三角形的内切圆与内心,等边三角形的面积,圆的面积,熟练掌握三角形内切圆的性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.方程x2-2012|x|+2013=0的所有实数根之和是( )
| A. | -2012 | B. | 0 | C. | 2012 | D. | 2013 |
 如图,一朵四瓣花飘动在10×10的网格中.
如图,一朵四瓣花飘动在10×10的网格中.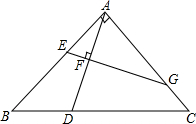 如图,等腰三角形ABC中,∠BAC=90°,AB=AC,点D在BC上,点F在AD上,过点F作EG⊥AD,交AB于E,AC于G,猜测AE,AG,BD,BC之间是否成比例,并说明理由.
如图,等腰三角形ABC中,∠BAC=90°,AB=AC,点D在BC上,点F在AD上,过点F作EG⊥AD,交AB于E,AC于G,猜测AE,AG,BD,BC之间是否成比例,并说明理由.