题目内容
13.方程x2-2012|x|+2013=0的所有实数根之和是( )| A. | -2012 | B. | 0 | C. | 2012 | D. | 2013 |
分析 先根据绝对值的意义分类讨论:当x>0时,原方程化为x2-2012x+2013=0;当x<0时,原方程化为x2+2012x+2013=0,然后根据根与系数的关系分别得到两个方程的两根之和,再求所有根之和.
解答 解:当x>0时,原方程化为x2-2012x+2013=0,方程的两根之和为2012;
当x<0时,原方程化为x2+2012x+2013=0,方程的两根之和为-2012,
所以方程x2-2012|x|+2013=0的所有实数根之和是0.
故选B.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.某玩具工厂只生产两种玩具:小狗和小汽车,工人小王的生产记录如表:
若小王某天工作了八小时,问他这天最多挣多少钱?(工厂对小王这天生产何种产品无限制、只有成品才有工资)
| 玩具小狗件数(单位:个) | 玩具小汽车个数(单位:个) | 总时间(单位:分) | 总工资(单位:元) |
| 1 | 1 | 35 | 2.15 |
| 2 | 2 | 70 | 4.30 |
| 3 | 2 | 85 | 5.05 |
18.设直线kx+(k+1)y-1=0(k为正整数)与两坐标轴所围成的三角形面积为Sk,k=1,2,…,2004,那么(S1+S2+…+S2004)等于( )
| A. | $\frac{1001}{2004}$ | B. | $\frac{1001}{1002}$ | C. | $\frac{2004}{2005}$ | D. | $\frac{1002}{2005}$ |
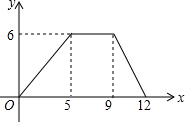 如图,是一对变量满足的函数关系的图象.有下列3个不同的问题情境:
如图,是一对变量满足的函数关系的图象.有下列3个不同的问题情境: 如图是由9个等边三角形拼成的六边形,若已知中间的小等边三角形的边长是2,则六边形的周长是60.
如图是由9个等边三角形拼成的六边形,若已知中间的小等边三角形的边长是2,则六边形的周长是60.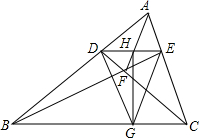 在△ABC中,D,E分别为AB,AC上一点,DE交AF于H,HG⊥BC,连接DG,GE.
在△ABC中,D,E分别为AB,AC上一点,DE交AF于H,HG⊥BC,连接DG,GE.