题目内容
15.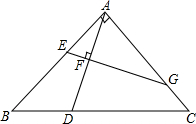 如图,等腰三角形ABC中,∠BAC=90°,AB=AC,点D在BC上,点F在AD上,过点F作EG⊥AD,交AB于E,AC于G,猜测AE,AG,BD,BC之间是否成比例,并说明理由.
如图,等腰三角形ABC中,∠BAC=90°,AB=AC,点D在BC上,点F在AD上,过点F作EG⊥AD,交AB于E,AC于G,猜测AE,AG,BD,BC之间是否成比例,并说明理由.
分析 过D作DM⊥AB于M,DN⊥AC与N,则四边形AMDN是矩形,根据矩形的性质得到∠1=∠2,由AF⊥EG,得到∠1=∠3,于是得到∠1=∠2=∠3,根据△ABC是等腰直角三角形,得到△BDM,△CDN是等腰直角三角形,根据等腰直角三角形的性质得到AN=MD,DN=NC,BD=$\sqrt{2}$MD,CD=$\sqrt{2}$NC,由于tan∠2=$\frac{BD}{CD}$=tan∠3=$\frac{AE}{AG}$,由于BC≠CD,于是得到AE,AG,BD,BC之间不能成比例.
解答 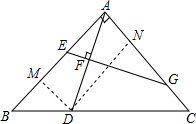 解:AE,AG,BD,BC之间不能成比例,
解:AE,AG,BD,BC之间不能成比例,
理由:过D作DM⊥AB于M,DN⊥AC与N,则四边形AMDN是矩形,
∴∠1=∠2,
∵AF⊥EG,
∴∠1=∠3,
∴∠1=∠2=∠3,
∵tan∠3=$\frac{AE}{AG}$,tan∠2=$\frac{AN}{DN}$,
∵△ABC是等腰直角三角形,
∴∠A=∠C=45°,
∴△BDM,△CDN是等腰直角三角形,
∴AN=MD,DN=NC,
∴BD=$\sqrt{2}$MD,CD=$\sqrt{2}$NC,
∴tan∠2=$\frac{BD}{CD}$,
∵∠2=∠3,
∴$\frac{AE}{AG}=\frac{BD}{CD}$,
∵BC≠CD,
∴$\frac{AE}{AG}≠\frac{BD}{BC}$,
∴AE,AG,BD,BC之间不能成比例.
点评 本题考查了相似三角形的判定和性质,等腰直角三角形的性质和判定,矩形的性质,正确的作出辅助线是解题的关键.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
7.下列分式中,最简分式是( )
| A. | $\frac{1-x}{2(x+1)}$ | B. | $\frac{x-2y}{{x}^{2}-4{y}^{2}}$ | C. | $\frac{x+1}{2{x}^{2}+4x+2}$ | D. | $\frac{x+3{x}^{2}}{{x}^{2}}$ |
4.一次函数y=(a-2)x+a-3的图象与y轴的交点在x轴的下方,则a的取值范围是( )
| A. | a≠2 | B. | a<3且a≠2 | C. | a>2且a≠3 | D. | a=3 |
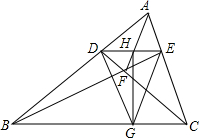 在△ABC中,D,E分别为AB,AC上一点,DE交AF于H,HG⊥BC,连接DG,GE.
在△ABC中,D,E分别为AB,AC上一点,DE交AF于H,HG⊥BC,连接DG,GE. 如图,在梯形ABCD中,AD∥BC,AB⊥BC,E是CD的中点,F在AB上,且∠1=∠2,AE、DF交于P,BE、CF交于Q,求证:四边形EPFQ是平行四边形.
如图,在梯形ABCD中,AD∥BC,AB⊥BC,E是CD的中点,F在AB上,且∠1=∠2,AE、DF交于P,BE、CF交于Q,求证:四边形EPFQ是平行四边形.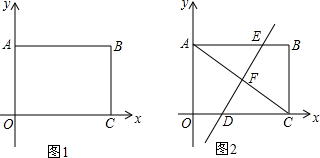
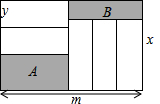 如图,长为m,宽为x(m>x)的大长方形被分割成7小块,除阴影A,B外,其余5块是形状、大小完全相同的小长方形,其较短一边长为y,记阴影A与B的面积差为S.
如图,长为m,宽为x(m>x)的大长方形被分割成7小块,除阴影A,B外,其余5块是形状、大小完全相同的小长方形,其较短一边长为y,记阴影A与B的面积差为S.