题目内容
13.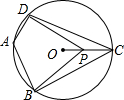 如图,四边形ABCD内接于⊙O,∠DAB=130°,连接OC,点P是半径OC上任意一点,连接DP,BP,则∠BPD可能为80度(写出一个即可).
如图,四边形ABCD内接于⊙O,∠DAB=130°,连接OC,点P是半径OC上任意一点,连接DP,BP,则∠BPD可能为80度(写出一个即可).
分析 连接OB、OD,根据圆内接四边形的性质求出∠DCB的度数,根据圆周角定理求出∠DOB的度数,得到∠DCB<∠BPD<∠DOB.
解答 解: 连接OB、OD,
连接OB、OD,
∵四边形ABCD内接于⊙O,∠DAB=130°,
∴∠DCB=180°-130°=50°,
由圆周角定理得,∠DOB=2∠DCB=100°,
∴∠DCB≤∠BPD≤∠DOB,即50°≤∠BPD≤100°,
∴∠BPD可能为80°,
故答案为:80.
点评 本题考查的是圆内接四边形的性质、圆周角定理,掌握圆内接四边形的对角互补是解题的关键.

练习册系列答案
相关题目
3.已知抛物线y=-x2-2x+3与x轴交于A、B两点,将这条抛物线的顶点记为C,连接AC、BC,则tan∠CAB的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | 2 |
4.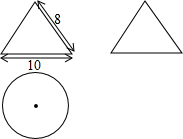 如图,按照三视图确定该几何体的全面积是(图中尺寸单位:cm)( )
如图,按照三视图确定该几何体的全面积是(图中尺寸单位:cm)( )
 如图,按照三视图确定该几何体的全面积是(图中尺寸单位:cm)( )
如图,按照三视图确定该几何体的全面积是(图中尺寸单位:cm)( )| A. | 40πcm2 | B. | 65πcm2 | C. | 80πcm2 | D. | 105πcm2 |
8.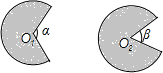 如图,阴影部分是两个半径为1的扇形,若α=120°,β=60°,则大扇形与小扇形的面积之差为( )
如图,阴影部分是两个半径为1的扇形,若α=120°,β=60°,则大扇形与小扇形的面积之差为( )
 如图,阴影部分是两个半径为1的扇形,若α=120°,β=60°,则大扇形与小扇形的面积之差为( )
如图,阴影部分是两个半径为1的扇形,若α=120°,β=60°,则大扇形与小扇形的面积之差为( )| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{5π}{3}$ | D. | $\frac{5π}{6}$ |
5.下列实数中小于0的数是( )
| A. | 2016 | B. | -2016 | C. | $\sqrt{2016}$ | D. | $\frac{1}{2016}$ |
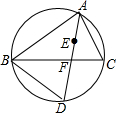 如图,点E是△ABC的内心,AE的延长线与BC相交于点F,与△ABC的外接圆相交于点D
如图,点E是△ABC的内心,AE的延长线与BC相交于点F,与△ABC的外接圆相交于点D 某校学生会为了解环保知识的普及情况,从该校随机抽取部分学生,对他们进行了垃圾分类了解程度的调查,根调查收集的数据绘制了如下的扇形统计图,其中对垃圾分类非常了解的学生有30人
某校学生会为了解环保知识的普及情况,从该校随机抽取部分学生,对他们进行了垃圾分类了解程度的调查,根调查收集的数据绘制了如下的扇形统计图,其中对垃圾分类非常了解的学生有30人