题目内容
 如图,AC=BC,∠ACB=90°,点D是AB的中点,点E是DC延长线上任意一点,CE=CF,∠ECF=90°,AE,BF相交于点G,AC,BF相交于点H.
如图,AC=BC,∠ACB=90°,点D是AB的中点,点E是DC延长线上任意一点,CE=CF,∠ECF=90°,AE,BF相交于点G,AC,BF相交于点H.(1)求证:AE=BF.
(2)判断AE与BF的位置关系,并证明.
(3)若BC=
| 2 |
| 3 |
| 4 |
考点:全等三角形的判定与性质,勾股定理
专题:
分析:(1)根据同角的余角相等求出∠BCF=∠ACE,然后利用“边角边”证明△ACE和△BCF全等,根据全等三角形对应边相等可得AE=BF;
(2)根据全等三角形对应角相等可得∠EAC=∠FBC,再求出∠AGH=90°,然后根据垂直的定义解答;
(3)利用勾股定理列式求出AB,再根据等腰直角三角形的性质求出CD=AD,然后利用勾股定理列式计算即可得解.
(2)根据全等三角形对应角相等可得∠EAC=∠FBC,再求出∠AGH=90°,然后根据垂直的定义解答;
(3)利用勾股定理列式求出AB,再根据等腰直角三角形的性质求出CD=AD,然后利用勾股定理列式计算即可得解.
解答:(1)证明:∵∠BCF=90°+∠ACF,∠ACE=90°+∠ACF,
∴∠BCF=∠ACE,
在△ACE和△BCF中,
,
∴△ACE≌△BCF(SAS),
∴AE=BF;
(2)解:AE⊥BF.
∵△ACE≌△BCF,
∴∠EAC=∠FBC,
∵∠AHG=∠CHB,∠ACB=90°,
∴∠AGH=∠BCH=90°,
∴AE⊥BF;
(3)解:∵∠ACB=90°,BC=
,
∴AB=
=2,
∵点D是AB的中点,
∴CD=AD=
AB=
×2=1,∠ADE=90°,
∴BF=AE=
=
=
.
∴∠BCF=∠ACE,
在△ACE和△BCF中,
|
∴△ACE≌△BCF(SAS),
∴AE=BF;
(2)解:AE⊥BF.
∵△ACE≌△BCF,
∴∠EAC=∠FBC,
∵∠AHG=∠CHB,∠ACB=90°,
∴∠AGH=∠BCH=90°,
∴AE⊥BF;
(3)解:∵∠ACB=90°,BC=
| 2 |
∴AB=
(
|
∵点D是AB的中点,
∴CD=AD=
| 1 |
| 2 |
| 1 |
| 2 |
∴BF=AE=
| AD2+DE2 |
12+(1+
|
| ||
| 4 |
点评:本题考查了全等三角形的判定与性质,勾股定理,熟记三角形全等的判定方法是解题的关键,难点在于求出∠BCF=∠ACE.

练习册系列答案
相关题目
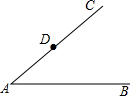 如图,已知∠CAB及边AC上一点D,在图中求作∠ADE,使得∠ADE与∠CAB是内错角,且∠ADE=∠CAB.(要求:尺规作图,不写作法,保留作图痕迹)
如图,已知∠CAB及边AC上一点D,在图中求作∠ADE,使得∠ADE与∠CAB是内错角,且∠ADE=∠CAB.(要求:尺规作图,不写作法,保留作图痕迹)
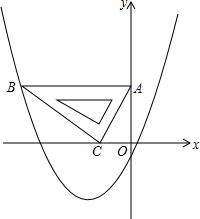 在平面直角坐标系中,现将一块含30°的直角三角板ABC放在第二象限,30°角所对的直角边AC斜靠在两坐标轴上,且点A(0,3),点C(-
在平面直角坐标系中,现将一块含30°的直角三角板ABC放在第二象限,30°角所对的直角边AC斜靠在两坐标轴上,且点A(0,3),点C(-
 如图,△ABC和△CDE为等腰Rt△,AC与DE相交于M点,AB和CD相交于N点,则对于下列结论:①AE=BD;②ED∥BC;③∠CNB=∠AMD,其中正确的结论有
如图,△ABC和△CDE为等腰Rt△,AC与DE相交于M点,AB和CD相交于N点,则对于下列结论:①AE=BD;②ED∥BC;③∠CNB=∠AMD,其中正确的结论有