题目内容
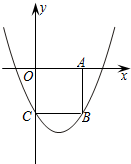 如图,在平面直角坐标系xOy中,边长为2的正方形OABC 的顶点A、C分别在x轴的正半轴和y轴的负半轴上,二次函数y=
如图,在平面直角坐标系xOy中,边长为2的正方形OABC 的顶点A、C分别在x轴的正半轴和y轴的负半轴上,二次函数y=| 2 |
| 3 |
(1)求该二次函数的解析式;
(2)结合函数的图象探索:当y>0时,x的取值范围.
考点:待定系数法求二次函数解析式,二次函数与不等式(组)
专题:
分析:(1)把B(2,-2),C(0,-2)代入y=
x2+bx+c得方程组,解出b,c的值,即可求出二次函数的解析式,
(2)令y=0,解得x的值,结合图象可知即可求出答案.
| 2 |
| 3 |
(2)令y=0,解得x的值,结合图象可知即可求出答案.
解答:解:(1)由题意得B(2,-2),C(0,-2)代入y=
x2+bx+c得
,解得
,
∴二次函数的解析式为y=
x2-
x-2;
(2)令y=0,得
x2-
x-2=0,解得x1=-1,x2=3,
结合图象可知:当x<-1或x>3时,y>0.
| 2 |
| 3 |
|
|
∴二次函数的解析式为y=
| 2 |
| 3 |
| 4 |
| 3 |
(2)令y=0,得
| 2 |
| 3 |
| 4 |
| 3 |
结合图象可知:当x<-1或x>3时,y>0.
点评:本题主要考查了待定系数法求二次函数解析式及二次函数与不等式,解题的关键是正确的求出二次函数的解析式.

练习册系列答案
 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案
相关题目
 在截面为半圆形的水槽内装有一些水,如图.水面宽AB为6分米,如果再注入一些水后,水面AB上升1分米,水面宽变为8分米,则该水槽截面直径为( )
在截面为半圆形的水槽内装有一些水,如图.水面宽AB为6分米,如果再注入一些水后,水面AB上升1分米,水面宽变为8分米,则该水槽截面直径为( )| A、5分米 | B、6分米 |
| C、8分米 | D、10分米 |
|-3|的相反数是( )
| A、-3 | B、|-3| |
| C、3 | D、|3| |
 如图,已知AB=DB,要使△ABC≌△DBC,还要添加什么条件?添加
如图,已知AB=DB,要使△ABC≌△DBC,还要添加什么条件?添加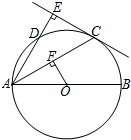 如图,AB为⊙O的直径,
如图,AB为⊙O的直径,
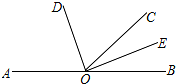 如图,点A、O、B在同一条直线上,射线OD与射线OE分别平分∠AOC和∠BOC
如图,点A、O、B在同一条直线上,射线OD与射线OE分别平分∠AOC和∠BOC