题目内容
 如图,CP、BP分别是∠DCA、∠ABD的平分线,求证:∠P=
如图,CP、BP分别是∠DCA、∠ABD的平分线,求证:∠P=| 1 |
| 2 |
考点:三角形内角和定理,三角形的外角性质
专题:证明题
分析:如图,证明∠DCO-∠ABO=∠A-∠D,此为解决该问题的关键结论;证明∠DCE=
∠DCO,∠PBE=
∠ABO,此为解决该问题的另一个关键结论;代入上式整理即可解决问题.
| 1 |
| 2 |
| 1 |
| 2 |
解答: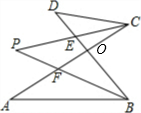 解:∵∠D+∠DCO+∠DOC=180°,
解:∵∠D+∠DCO+∠DOC=180°,
∠A+∠ABO+∠AOB=180°,而∠DOC=∠AOB,
∴∠D+∠DCO=∠A+∠ABO,
∴∠DCO-∠ABO=∠A-∠D;
同理可证:∠P+∠PBE=∠D+∠DCE,
∴∠P=∠D+∠DCE-∠PBE;
∵CP、BP分别是∠DCA、∠ABD的平分线,
∴∠DCE=
∠DCO,∠PBE=
∠ABO,
∴∠P=∠D+
∠DCO-
∠ABO=∠D+
,
∴∠P=
(∠A+∠D).
 解:∵∠D+∠DCO+∠DOC=180°,
解:∵∠D+∠DCO+∠DOC=180°,∠A+∠ABO+∠AOB=180°,而∠DOC=∠AOB,
∴∠D+∠DCO=∠A+∠ABO,
∴∠DCO-∠ABO=∠A-∠D;
同理可证:∠P+∠PBE=∠D+∠DCE,
∴∠P=∠D+∠DCE-∠PBE;
∵CP、BP分别是∠DCA、∠ABD的平分线,
∴∠DCE=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠P=∠D+
| 1 |
| 2 |
| 1 |
| 2 |
| ∠A-∠D |
| 2 |
∴∠P=
| 1 |
| 2 |
点评:该题主要考查了三角形的内角和定理、角平分线的性质及其应用问题;解题的关键是深入观察图形,准确找出图形中隐含的数量关系,灵活解题.

练习册系列答案
相关题目
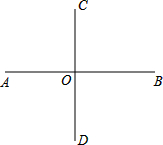 如图,已知AB⊥CD于点O,点E为平面内一点,且∠BOE=60°
如图,已知AB⊥CD于点O,点E为平面内一点,且∠BOE=60°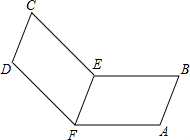 如图,取一张长方形的硬纸板ABCD,将硬纸板ABCD对折使CD与AB重合,EF为折痕.把长方形ABEF平放在桌面上,另一个面CDEF无论怎么改变位置总有CD∥AB存在,你知道为什么吗?
如图,取一张长方形的硬纸板ABCD,将硬纸板ABCD对折使CD与AB重合,EF为折痕.把长方形ABEF平放在桌面上,另一个面CDEF无论怎么改变位置总有CD∥AB存在,你知道为什么吗? 找出图中所有的同位角、内错角、同旁内角.
找出图中所有的同位角、内错角、同旁内角.