题目内容
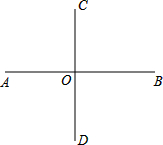 如图,已知AB⊥CD于点O,点E为平面内一点,且∠BOE=60°
如图,已知AB⊥CD于点O,点E为平面内一点,且∠BOE=60°(1)∠COE=
(2)画OF平分∠COE,OG平分∠BOE,则∠FOG=
(3)在(2)的条件下,若将题目中∠BOE=60°改成∠BOE=a°(a>90),其他条件不变,你能求出∠FOG的度数吗?若能,请你写出求解过程;若不能,请说明理由.
考点:垂线,角平分线的定义
专题:
分析:(1)根据余角的性质,可得答案;
(2)根据角平分线的性质,可得∠EOF、∠EOG的度数,根据角的和差,可得答案;
(3)根据角平分线的性质,可得∠EOF、∠EOG的度数,根据角的和差,可得答案.
(2)根据角平分线的性质,可得∠EOF、∠EOG的度数,根据角的和差,可得答案;
(3)根据角平分线的性质,可得∠EOF、∠EOG的度数,根据角的和差,可得答案.
解答: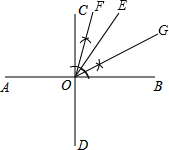 解:(1)由于角的性质,得∠COE=90°-∠BOE=90°-60°=30°,
解:(1)由于角的性质,得∠COE=90°-∠BOE=90°-60°=30°,
∠COE=∠COB+∠BOE=90°+60°=150°
(2)由OF平分∠COE,OG平分∠BOE,得
∠EOF=
∠COE=
×30=15°,∠EOG=
∠BOE=
×60°=30°.
由角的和差,得∠FOG=∠EOF+∠EOG=15°+30°=45°,
故答案为:30,或150;45;
(3)能,理由如下:
由OF平分∠COE,OG平分∠BOE,得
∠EOF=
∠COE,∠EOG=
∠BOE.
由角的和差,得∠FOG=∠EOF+∠EOG=
∠COE+
∠BOE=
∠BOC=
×90°=45°.
 解:(1)由于角的性质,得∠COE=90°-∠BOE=90°-60°=30°,
解:(1)由于角的性质,得∠COE=90°-∠BOE=90°-60°=30°,∠COE=∠COB+∠BOE=90°+60°=150°
(2)由OF平分∠COE,OG平分∠BOE,得
∠EOF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
由角的和差,得∠FOG=∠EOF+∠EOG=15°+30°=45°,
故答案为:30,或150;45;
(3)能,理由如下:
由OF平分∠COE,OG平分∠BOE,得
∠EOF=
| 1 |
| 2 |
| 1 |
| 2 |
由角的和差,得∠FOG=∠EOF+∠EOG=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了垂线,利用了垂线的定义,角平分线的定义,角的和差.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
 如图,点A、B、C都在⊙O上,若∠A=45°,∠B=60°,则∠ACO的度数为( )
如图,点A、B、C都在⊙O上,若∠A=45°,∠B=60°,则∠ACO的度数为( )| A、10° | B、15° |
| C、20° | D、30° |
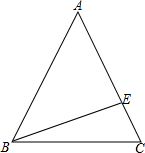 如图,在等腰△ABC中,AB=AC=5,BC=6.
如图,在等腰△ABC中,AB=AC=5,BC=6.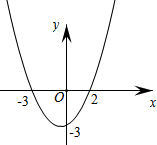 如图抛物线y=ax2+bx+c与x轴交于点(-3,0)、(2,0),与y轴交于点(0,-3),结合图象回答.
如图抛物线y=ax2+bx+c与x轴交于点(-3,0)、(2,0),与y轴交于点(0,-3),结合图象回答. 如图,CP、BP分别是∠DCA、∠ABD的平分线,求证:∠P=
如图,CP、BP分别是∠DCA、∠ABD的平分线,求证:∠P=