题目内容
11. 如图,已知CD⊥AB,垂足为D,EF⊥AB,垂足为F.
如图,已知CD⊥AB,垂足为D,EF⊥AB,垂足为F.(1)求证:CD∥EF;
(2)如果∠1=∠2,且∠3=115°,求∠ACB的度数.
分析 (1)由“CD⊥AB,EF⊥AB”可得出∠CDB=∠EFB=90°,再由“同位角相等,两直线平行”即可得出结论;
(2)由CD∥EF可得出∠2=∠BCD,再由∠1和∠2的关系可得出∠1=∠BCD,根据“内错角相等,两直线平行”即可得出DG∥BC,从而得出∠ACB=∠3=115°.
解答 (1)证明:∵CD⊥AB,EF⊥AB,
∴∠CDB=90°,∠EFB=90°,
∴∠CDB=∠EFB=90°,
∴CD∥EF.
(2)解:∵CD∥EF,
∴∠2=∠BCD,
又∵∠1=∠2,
∴∠1=∠BCD,
∴DG∥BC,
∴∠ACB=∠3=115°
点评 本题考查了平行线的判定及性质,解题的关键是根据同位角(内错角)相等证出两直线平行.本题属于基础题,难度不大,解决该题型题目时,根据角的关系证出直线平行是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.下列各方程中,是一元一次方程的是( )
| A. | x-2y=4 | B. | xy=4 | C. | 3y-1=4 | D. | $\frac{1}{4}x-4$ |
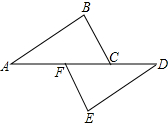 如图,点A、F、C、D在同一直线上,点B和E分别在直线AD的两侧,AB∥DE且AB=DE,AF=DC.
如图,点A、F、C、D在同一直线上,点B和E分别在直线AD的两侧,AB∥DE且AB=DE,AF=DC.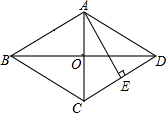 如图,已知菱形ABCD的对角线AC与BD相交于点O,AE垂直且平分边CD,垂足为E,求∠BCD的度数.
如图,已知菱形ABCD的对角线AC与BD相交于点O,AE垂直且平分边CD,垂足为E,求∠BCD的度数. 如图,用两张等宽的长方形纸条,随意交叉放在一起,重合的部分构成了一个四边形ABCD,试证明四边形ABCD是菱形.
如图,用两张等宽的长方形纸条,随意交叉放在一起,重合的部分构成了一个四边形ABCD,试证明四边形ABCD是菱形.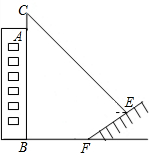 如图,某校有一教学楼AB,其上有一避雷针AC为7米,教学楼后面有一小山,其坡度为i=$\sqrt{3}$:1,山坡上有一休息亭供爬山人员休息,测得山坡脚F与教学搂的水平距离BF为19米,与休息亭的距离FE为10米,从休息亭E测得教学楼上避雷针顶点C的仰角为30°,求教学搂AB的高度.(结果保留根号)(注:坡度i是指坡面的铅直高度与水平宽度的比)
如图,某校有一教学楼AB,其上有一避雷针AC为7米,教学楼后面有一小山,其坡度为i=$\sqrt{3}$:1,山坡上有一休息亭供爬山人员休息,测得山坡脚F与教学搂的水平距离BF为19米,与休息亭的距离FE为10米,从休息亭E测得教学楼上避雷针顶点C的仰角为30°,求教学搂AB的高度.(结果保留根号)(注:坡度i是指坡面的铅直高度与水平宽度的比)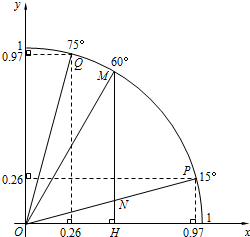 如图,点P、M、Q在半径为1的⊙O上,根据已学知识和图中数据(0.97、0.26为近似数),解答下列问题:
如图,点P、M、Q在半径为1的⊙O上,根据已学知识和图中数据(0.97、0.26为近似数),解答下列问题: