题目内容
19.(1)分解因式:2ma2-8mb2;(2)解方程:$\frac{x}{x-1}$+1=$\frac{3}{2x-2}$.
分析 (1)原式提取公因式,再利用平方差公式分解即可;
(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)原式=2m(a2-4b2)=2m(a+2b)(a-2b);
(2)去分母得:2x+2x-2=3,
解得:x=$\frac{5}{4}$,
经检验x=$\frac{5}{4}$是分式方程的解.
点评 此题考查了解分式方程,利用了转化的思想,解分式方程注意要进行检验.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
7.已知一个立体图形的三视图如图所示,那么它是( )
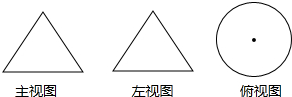

| A. | 圆锥 | B. | 球 | C. | 圆柱 | D. | 棱柱 |
4.下列各组数中,以它们为边长的线段不能构成直角三角形的是( )
| A. | 1,$\sqrt{2}$,$\sqrt{3}$ | B. | 2,3,$\sqrt{6}$ | C. | 5,12,13 | D. | $\frac{5}{4}$,1,$\frac{3}{4}$ |
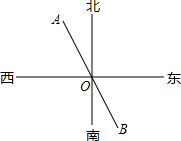 如图所示,已知点A,O,B在同一条直线上,若OA的方向是北偏西26°,则OB的方向是南偏东26°.
如图所示,已知点A,O,B在同一条直线上,若OA的方向是北偏西26°,则OB的方向是南偏东26°.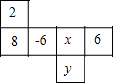 一个正方体的相对的面上所标的两个数,都是互为相反数的两个数,如图是这个正方体的展开图,那么x+y的值为-10.
一个正方体的相对的面上所标的两个数,都是互为相反数的两个数,如图是这个正方体的展开图,那么x+y的值为-10.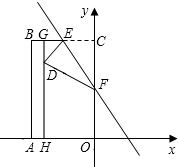 如图,矩形OABC在平面直角坐标系内(O为坐标原点),点A在x轴上,点C在y轴上,点B的坐标为(-4,6),点E是BC的中点,点H在OA上,且AH=1,过点H且平行于y轴的HG与EB交于点G,现将矩形折叠,使顶点C落在HG上,并与HG上的点D重合,折痕为EF,点F为折痕与y轴的交点.CF=2$\sqrt{3}$.
如图,矩形OABC在平面直角坐标系内(O为坐标原点),点A在x轴上,点C在y轴上,点B的坐标为(-4,6),点E是BC的中点,点H在OA上,且AH=1,过点H且平行于y轴的HG与EB交于点G,现将矩形折叠,使顶点C落在HG上,并与HG上的点D重合,折痕为EF,点F为折痕与y轴的交点.CF=2$\sqrt{3}$. 如图,已知CD⊥AB,垂足为D,EF⊥AB,垂足为F.
如图,已知CD⊥AB,垂足为D,EF⊥AB,垂足为F.